《图》专题

关于图的算法。

1. 图的存储

稠密图用邻接矩阵存储，稀疏图用邻接表存。
有向图和无向图算法区别只在读取边的时候：是读一条单向边，还是正反双向一次读两条边。

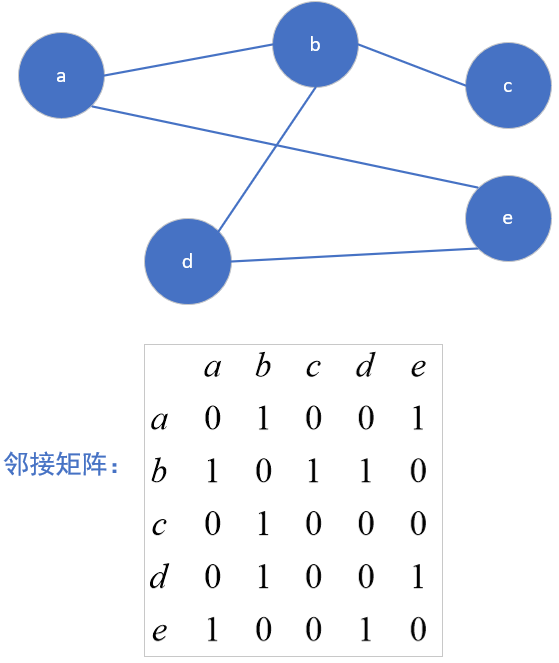
1.1 邻接矩阵

1.1.1 邻接矩阵表示无向图

假如一个图有n个顶点，则开n×n的邻接矩阵，若顶点i到顶点j存在一条边，则g[i][j] = 1，否则为0.

无向图的邻接矩阵一定是对称矩阵。
无向图中某节点的度就是其对应行或列所有非0元素之和。

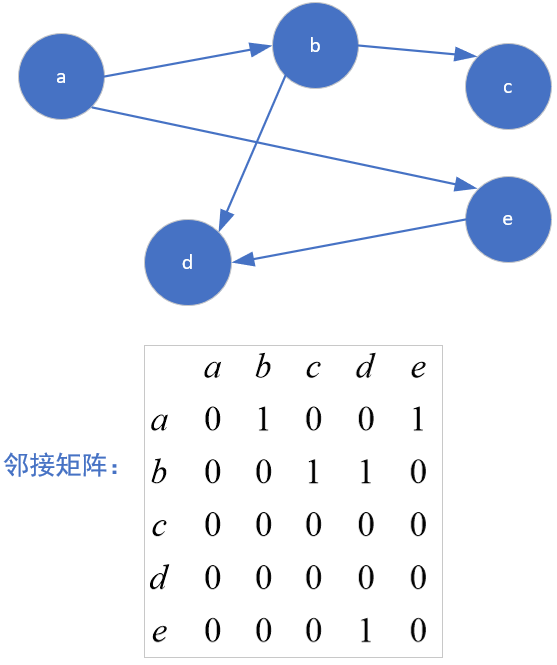
1.1.2 邻接矩阵表示有向图

有向图中某顶点：
对应行的非0元素之和为出度
对应列的非0元素之和为入度

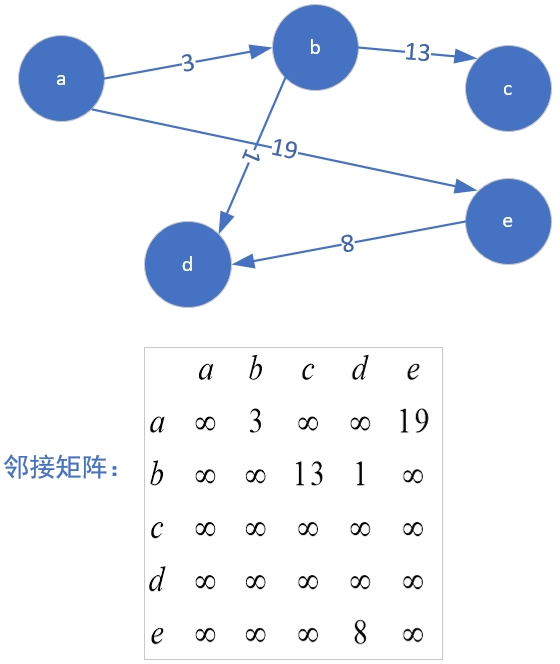
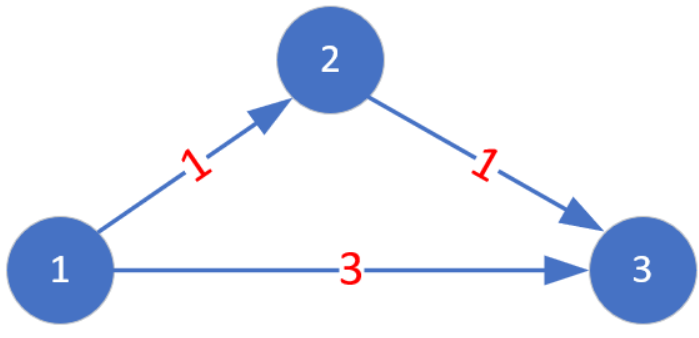
1.1.3 邻接矩阵表示网

网就是边具有非0非1权值的图，若顶点i到顶点j存在一条边，且该边的权值为w，则g[i][j] = w，否则为无穷大.

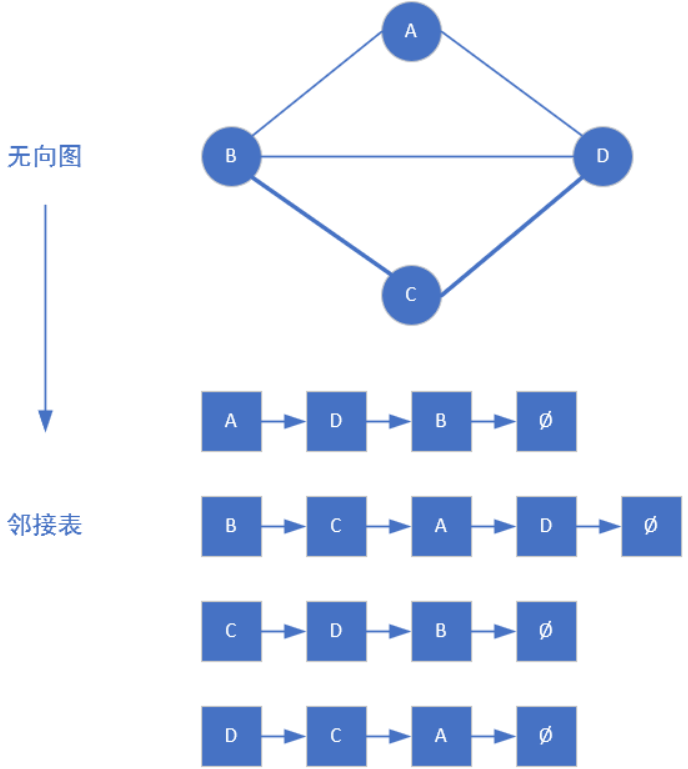
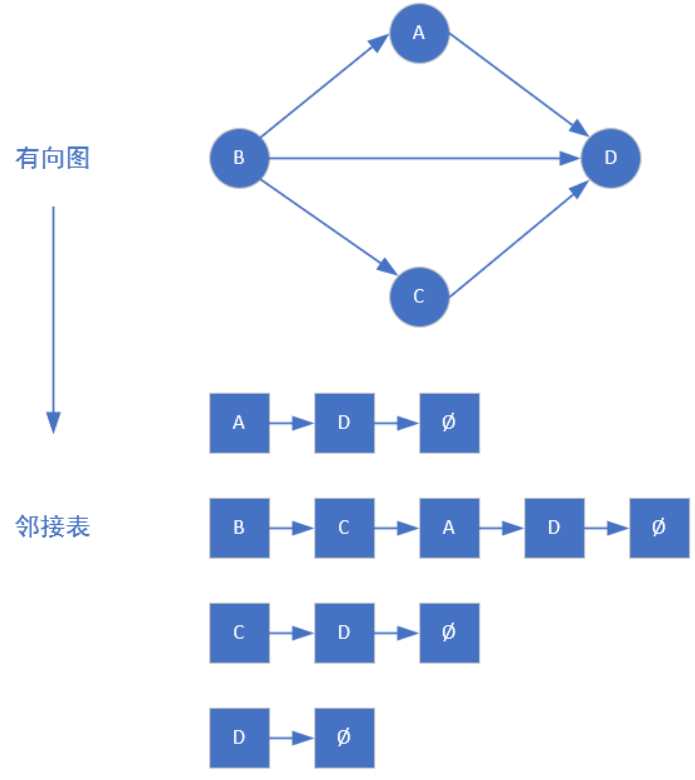
1.2 邻接表

邻接表是一组链表的集合，其中每一个链表的头节点都代表图中某个顶点，该链表上的其他节点代表该顶点的邻居。链表中的每一个节点有两个属性，一个是next，指向该链表头节点的另一个儿子，另一个属性是该节点的编号/值。

1.2.1 邻接表表示无向图

1.2.2 邻接表表示有向图

邻接表的结构与哈希表的拉链法结构一模一样，都是链表类型的数组。

2. 遍历

2.1 深度优先遍历

一直往深处走，直到无路可走时，才会退回寻找其他路径。

用两个经典问题来说明这个算法

2.1.1 全排列

【题目】

输入正整数n，打印1~n的全排列

https://www.acwing.com/problem/content/844/

【解析】

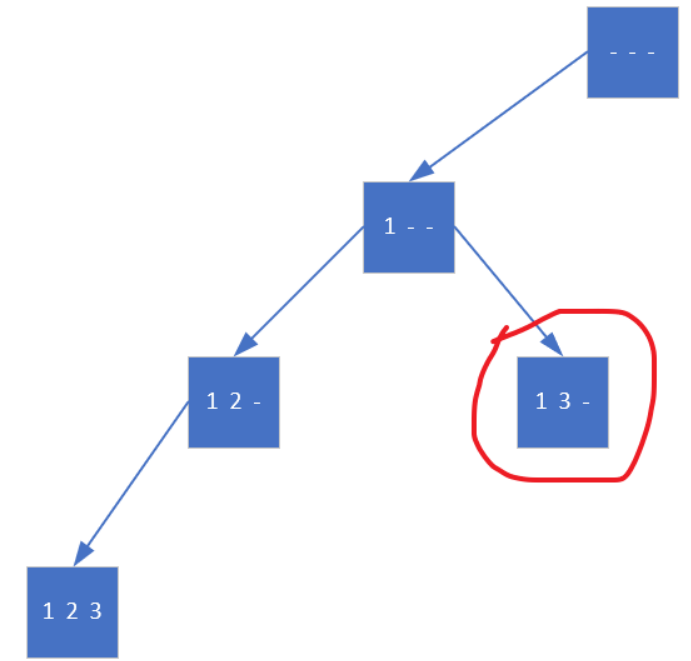
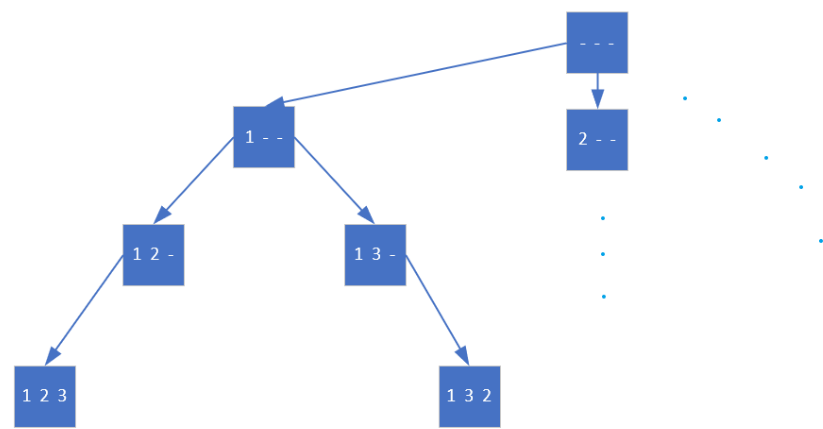
比如n=3，一开始有三个空位可以填

假如第一个位置选择填1

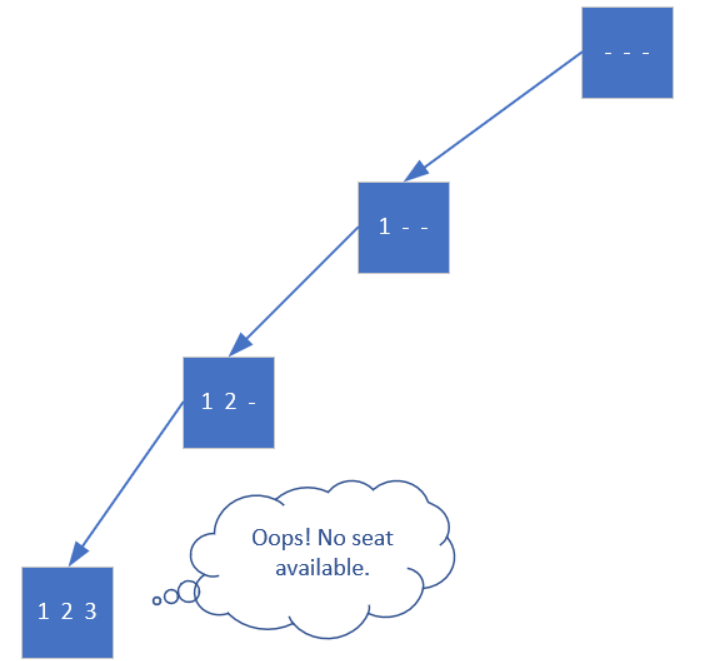
dfs会继续在此基础上决定第二个位置填几，因为是深度优先，优先往深处搜，不撞南墙是不会回头的。所以现在还剩两个位置可填。
继续往深处搜索，直到位置填满

这时它意识到自己已经无法前进了，只好回退一步看看有没有别的路。退回到【1 2 _】处后，它发现也没有别的选择了，刚才3也选过了，只能再回退一步到【1 _ _】，检查发现，第二个位置不光可以填2，还可以填3

继续重复上述步骤，直到退回根节点

【ac代码】

class Solution {
    final int N = 10; //最多求10位数字的全排列
    int[] path = new int[N]; //记录当前全排列
    boolean[] visited = new boolean[N]; //记录某个数字是否已经被填过，填过为true

    public void dfs(int level, int n) { //level代表现在填到第几个空位了，n代表求1~n的全排列
        if(level == n){ //如果撞到南墙，等于已经填好了一个完整的全排列，将其输出后返回
            for (int i = 0; i < n; i++) {
                System.out.print(path[i]);
            }
            System.out.println();
            return;
        }

        for (int i = 1; i <= n; i++) { //每一层可以填的数字：1、2、3、...、n
            if(!visited[i]){ //如果i还没有被填过
                path[level] = i; //填上
                visited[i] = true; //将i标记为已填过
                dfs(level+1, n); //本空位填写完成，尝试填写下一空位

                //递归开始回溯，恢复现场
                path[level] = 0;
                visited[i] = false;
            }
        }
    }

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        Solution s = new Solution();
        s.dfs(0,n);
    }
}

2.1.2 n皇后

【题目】

https://www.acwing.com/problem/content/845/

一个n*n的棋盘上，任意两个棋子不能出现在同一行或同一列或同一斜线。输出所有可能的方案。

【ac代码】

第一种方法是按照全排列的思路来解

#include<iostream>
using namespace std;

const int N = 20;     //因为有对角线的存在，一个n*n的棋盘对角线有2n-1条，稍微开大点
bool col[N], dg[N], udg[N];     //col表示该列是否存在棋子，dg表示主对角线，udg表示副对角线
char chessBoard[N][N];      //棋盘
int n;                  //用户输入棋盘的大小

void dfs(int row)
{
    
    if(row == n) //深搜触底了，即得到了一个完整的有效的棋子摆放棋盘
    {
        for(int i = 0;i<n;i++)  //打印当前棋盘
        {
            for(int j = 0;j<n;j++) printf("%c",chessBoard[i][j]);
            printf("\n");
        }
        printf("\n");
        return;
    }
    
    for(int i = 0;i<n;i++)  //i表示棋盘的列，一共有n列
    {
        /*
          col[i}是看i这列是否无棋子，
          dg[i+row]看i和row所处的主对角线是否无棋子，
          udg[i-row+n]看i和row所处的副对角线是否无棋子
          用i+row和i-row+n为啥能表示对角线在下面有详细解释
        */
        if(!col[i]&&!dg[i+row]&&!udg[i-row+n])
        {
            chessBoard[row][i] = 'Q';   //在(row, i)这个位置落子
            col[i] = dg[i+row] = udg[i-row+n] = true; //将(row, i)这个位置所处的【列】和【主副对角线】标识为已占用
            dfs(row+1); //进入下一行
            
            /*恢复现场*/
            col[i] = dg[i+row] = udg[i-row+n] = false;
            chessBoard[row][i] = '.';
        }
    }
}

int main()
{
    scanf("%d",&n);
    for(int i =0;i<n;i++) //初始化棋盘
    {
        for(int j = 0;j<n;j++) chessBoard[i][j] = '.';
    }
    dfs(0);
    return 0;
    
}

用i+row和i-row+n为啥能表示对角线？

i在我们的代码中表示列，row代表行，那么对角线就可以用y=x+b来表示。
又因为对角线的斜率都相等，则b就可以唯一的标识一条对角线了。
主对角线斜率为1，b = y-x，为了防止出现负数，我们把他加上n，因此【i-row+n】就表示主对角线。
副对角线斜率为-1，b = y+x，因此【i+row】就表示副对角线。

第二种解法是遍历整个棋盘，在每个位置判断放还是不放。

#include<iostream>
using namespace std;

const int N = 20;     //因为有对角线的存在，一个n*n的棋盘对角线有2n-1条，稍微开大点
bool row[N], col[N], dg[N], udg[N];     //dg表示主对角线，udg表示副对角线
char chessBoard[N][N];      //棋盘
int n;                  //用户输入棋盘的大小

/*棋盘的(x, y)位置，chessCount代表已经放了几个棋子*/
void dfs(int x, int y, int chessCount)
{
    if(y>=n) y = 0, x++; //如果一行走到头了，就进入下一行
    if(x==n) //如果棋盘已经遍历完了
    {
        if(chessCount == n) //若已放置的棋子数等于n，代表找到了一个n皇后方案
        {
            for(int i = 0;i<n;i++)//输出棋盘
            {
                for(int j = 0;j<n;j++) printf("%c",chessBoard[i][j]);
                printf("\n");
            }
            printf("\n");
        }
        return;
    }
    
    //一步步递归先走到了棋盘最后的位置
    dfs(x,y+1,chessCount);
    
    //弹栈，在每一步检查该位置是否可以放置棋子
    if(!row[x]&&!col[y]&&!dg[y+x]&&!udg[y-x+n])
    {
        chessBoard[x][y] = 'Q';
        row[x] = col[y] = dg[y+x] = udg[y-x+n] = true;
        dfs(x,y+1,chessCount+1);
        
        /*恢复现场*/
        row[x] = col[y] = dg[y+x] = udg[y-x+n] = false;
        chessBoard[x][y] = '.';
    }
    
    
}

int main()
{
    scanf("%d",&n);
    for(int i =0;i<n;i++) //初始化棋盘
    {
        for(int j = 0;j<n;j++) chessBoard[i][j] = '.';
    }
    dfs(0, 0, 0);
    return 0;
    
}

对比来看，显然按照全排列思路的第一种方法效率更高，好好体会下二者的区别。

2.2 宽度优先遍历

从起点开始逐层向外拓展。

宽度优先队列一般依靠队列完成（比如树的层序遍历）

2.2.1 走迷宫

【题目】

https://www.acwing.com/problem/content/846/

0表示路，1表示墙，在01组成的迷宫中，找出一条从左上角到右下角的最短路。

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;

typedef pair<int, int> PII;
const int N = 200;
bool maze[N][N]; //迷宫
int distan[N][N]; //走到某个点需要的最小步数
int n, m; //用户输入的棋盘大小n*m

/*用于模拟上下左右，代码后有详细介绍*/
int dx[4] = {-1,0,1,0};
int dy[4] = {0,-1,0,1};


int bfs()
{
    memset(distan, -1, sizeof(distan)); //将所有点到迷宫左上角（起点）的距离初始化为-1
    distan[0][0] = 0; //第一个点到它自己所在位置的距离为0
    
    queue<PII> q; //用来装迷宫的每一个点（类型为pair）
    q.push({0, 0}); //先把起点给放进去
    
    while(!q.empty())//只要队列不为空
    {
        /*取出队头*/
        PII head = q.front(); 
        q.pop(); 
        
        for(int i = 0;i<4;i++) //判断队头所在位置的上下左右是否有路可走
        {
            /*选一个方向，走到其位置上*/
            int x = head.first+dx[i];
            int y = head.second+dy[i];
            /*如果这个位置是合法的（distan[x][y]==1判断该点是否已经走过，max[x][y]判断该位置是墙还是路）*/
            if(x>=0&&x<n&&y>=0&&y<m&&distan[x][y]==-1&&maze[x][y]==0)
            {
                distan[x][y] = distan[head.first][head.second]+1; //将这个位置记录下来
                q.push({x, y}); //将这个点加入到队列中，等待后续处理
            }
        }
    }
    return distan[n-1][m-1];
}

int main()
{
    scanf("%d %d",&n,&m);
    for(int i= 0;i<n;i++) //接收棋盘
    {
        for(int j = 0;j<m;j++) scanf("%d",&maze[i][j]);
    }
    printf("%d", bfs());
    return 0;
}

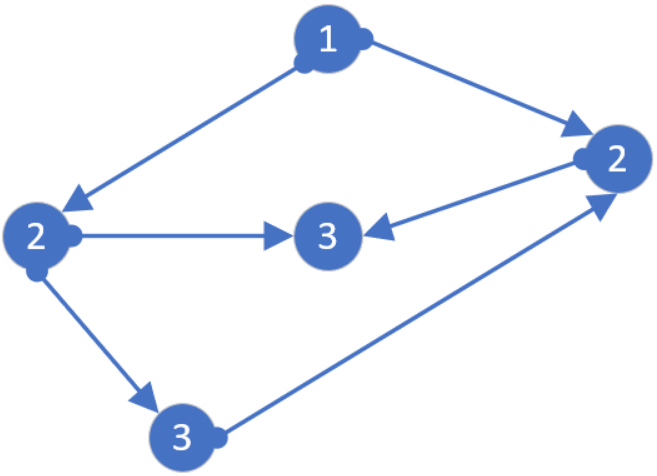
手动模拟一下该算法

可以看出宽搜是齐头并进的地毯式搜索

当所有边的权值为1时，如本题，可以用宽搜来求最短路，其他情况有专门的最短路算法

【本题中还有一个遍历矩阵某位置的上下左右的技巧点】

对一个点(x, y)：
(x+1, y)走到它的右边
(x-1, y)走到它的左边
(x, y+1)走到它的上边
(x, y-1)走到它的下边要利用这性质方便的遍历它的上下左右四个位置，方法如下：
先定义这样一个数组

int dx[4] = {-1,0,1,0}; 
int dy[4] = {0,-1,0,1};

然后用一个循环即可遍历(x, y)的上下左右

for(int i = 0;i<4;i++)
{
    int tempX = x+dx[i];
    int tempY = y+dy[i];
    action on (tempX, tempY);
}

2.3 树和图的遍历

树是有向无环图，但有向无环图不一定是树，因为可能有两个顶点的出边指向同一个顶点。

本节我们采用邻接表存图。

2.3.1 深度优先遍历

int dfs(int u)
{
    st[u] = true; // st[u]表示点u已经被遍历过

    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i]; //节点i的编号
        if (!st[j]) dfs(j);
    }
}

比如通过深度优先遍历来求多叉树的总结点数。

/*
该函数求以任一节点u为根节点的多叉树的节点总数
*/
int dfs(int u)
{
    st[u] = true; //将节点u标为已访问过
    int sum = 1;  //节点总数
    for(int i = h[u]; i!=-1;i= ne[i])//以节点u为根节点遍历整个子树
    {
        int j = e[i];  //获取节点i的编号
        if(st[j]) continue; //如果该节点被访问过，就跳出本次循环
        
        int s = dfs(j); //先深入到树的最深处
        sum+=s; //弹栈后不断累加计算当前位置子树的总节点数
    }
    return sum; //当递归栈全部弹出后，sum就是以u为根节点子树的总节点数
}

再通过一个例题来理解。

【题目】

树的重心

https://www.acwing.com/problem/content/848/

【解析】

先引入一些必要的概念

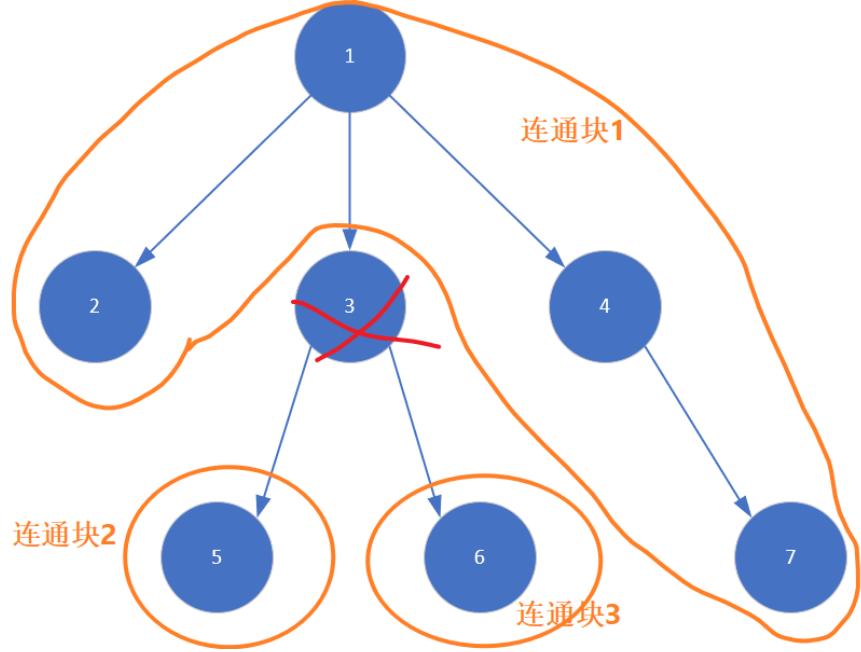
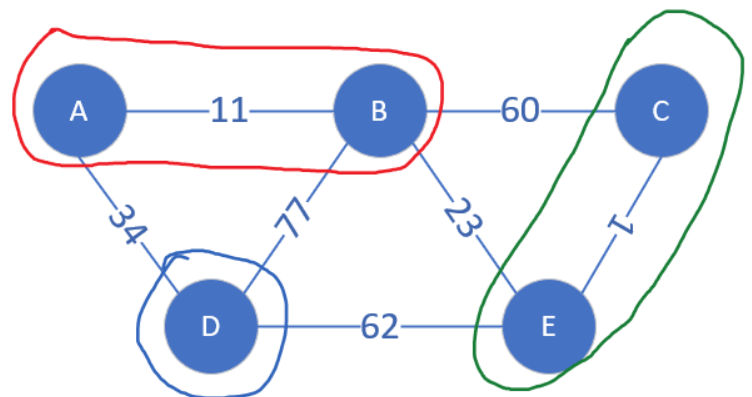
连通块

假如把3号节点删掉，整棵树就被分成了三个连通块。

重心

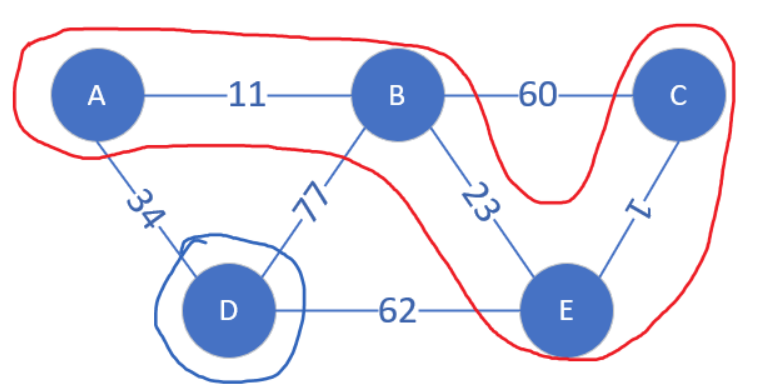
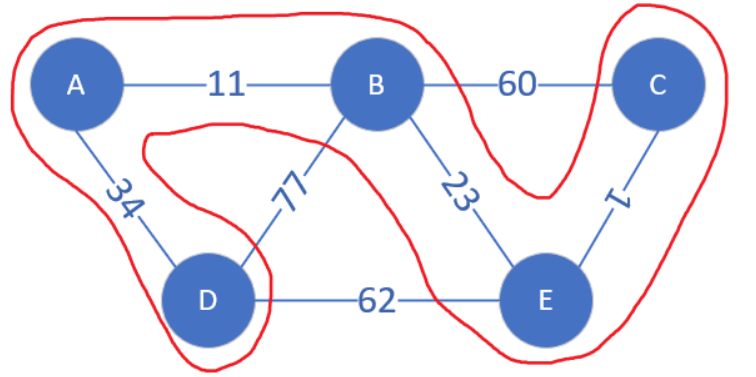
找出树中的某个节点，如果把这个节点删掉后，划分出的所有连通块的最大值最小（即划分的最平均），则这个点就被称为重心。当树的总结点数为偶数时，可能有多个重心。

要解决本题，我们需要把所有节点逐个假设为重心，测试每一种假设中最大连通块的大小，完成后最小的那个就是我们要的答案。
这道题可以基于上面dfs计算总结点数的方法来做：

#include<iostream>
#include<cstring>
using namespace std;

const int N = 1e5, M = N*2;
int e[M], ne[M], idx, h[M];     //用邻接表来表示图
bool st[M];                     //表示某个节点是否被访问过了
int n;                          //用户输入的树的总节点数
int ans = 0x3f3f3f3f;           //答案

void add(int a, int b)          //创建一条边a->b（有向）
{
    /*邻接表类似于哈希数组的拉链结构，每一条链上加入新元素使用头插法*/
    e[idx] = b;                 //模拟申请新节点，其编号为b
    ne[idx] = h[a];             //将刚申请的新节点next指针指向邻接表中编号a开头链表的头节点
    h[a] = idx++;               //然后让新节点成为该链表的头节点
}

/*返回以编号u为根节点的子树的总节点数*/
int dfs(int u) 
{
    st[u] = true;                       //将u节点标识为已使用
    int sum = 0, res = 0;               //sum用于计算u的【子节点】总数，res中存放最大的【连通块大小】
    for(int i = h[u]; i!=-1;i = ne[i])  //遍历u的子节点，计算其总的子节点数
    {
        int j = e[i];                   //i现在相当于是指向节点的指针，e[i]获得节点i的编号
        if(st[j]) continue;             //如果节点i已经被遍历过，就continue
        
        int s = dfs(j);                 //dfs到树的最深处
        res = max(s, res);              //开始弹栈，每次s都是当前根节点为j的子树的总节点数
        sum+=s;                         //计算当前子树的总节点数, 注意这里不会产生重复计算，因为邻接表中某一链表（比如a->b->c->d），bcd都是a的下一代，都分属在不同的子树，每一次弹栈，都会弹到一个完全不同的子树上去。
    }
    res = max(res, n-sum-1);            //取【子树的总节点数】与【子树之外的连通块大小】中较大的值
    ans = min(ans, res);                //对每一个假定的重心，比较它们的最小连通块大小，最小的即是答案
    return sum+1;
}


int main()
{
    memset(h, -1, sizeof(h));   //初始化邻接表的所有头结点
    scanf("%d",&n);
    int a=0,b=0;
    for(int i =0;i<n-1;i++)     //一共n-1条无向边
    {
        scanf("%d%d",&a,&b);
        add(a, b);              //无向边用双向边模拟
        add(b, a);
    }
    dfs(1);                     //编号为1的节点开始, 不过因为结构其实是无向图，因此从任意编号开始都是可以的
    printf("%d",ans);
    return 0;
}

2.3.2 宽度优先遍历

【题目】

https://www.acwing.com/problem/content/849/

给定一个n个点m条边的有向图，图中可能存在重边和自环。所有边的长度都是1，点的编号为1~n。请你求出1号点到n号点的最短距离，如果从1号点无法走到n号点，输出-1。

【解析】

先引入必要的改概念：

重边

自环

题目条件给出所有边的长度都为1，因此我们可以用宽搜来求最短距离

只需要对最基本的深搜框架做一些改动即可。

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N = 1e5+10;

int ne[N], h[N], e[N], idx; //邻接表
int d[N];       //编号为i的节点与起点之间的最短距离
int n, m;       //用户输入的节点数和边数
void add(int a, int b) //添加一条边
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

int bfs()
{
    queue<int> q;
    q.push(1);  //1号节点为起点
    d[1] = 0;   //1号节点与它自己的距离为0
    while(!q.empty())
    {
        /*弹出当前队列头，里面的值是某一个节点的编号*/
        int fore = q.front(); 
        q.pop();
        
        for(int i = h[fore]; i!=-1; i = ne[i]) //遍历某一个节点所有的儿子，i相当于节点指针
        {
            int succ = e[i];   //取出节点i中的值，也就是节点的编号
            if(d[succ]==-1)    //如果当前节点与起点之间的距离还未被更新过（即它还没有被遍历过）
            {
                d[succ] = d[fore]+1;   //添加当前节点与起点之间的距离信息 => 它的父节点距离+1
                q.push(succ);  //将刚更新的节点push到队列中，之后还要以它为父节点遍历其子节点（如果有）
            }
        }
    }
    return d[n];    //返回最后一个节点与起点之间的距离
}

int main()
{
    /*将所有邻接表的表头，距离数组初始化*/
    memset(h, -1, sizeof(h));
    memset(d, -1, sizeof(d));
    
    scanf("%d%d",&n,&m);
    int a,b;
    for(int i = 0;i<m;i++)
    {
        scanf("%d%d",&a,&b);
        add(a,b);
    }
    printf("%d\n",bfs());
    return 0;
}

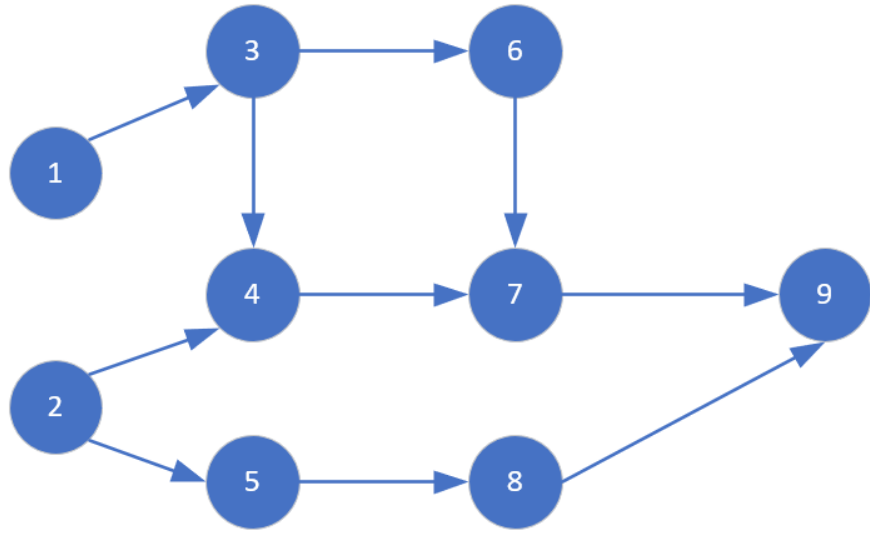
2.3.3 拓扑排序

拓扑序列: 给定一个有向图，若以该图为准找出一种节点序列，这个序列从左往右的顺序在图中可以【顺着箭头】遍历所有节点，那么这个序列就称为该有向图的拓扑序列（不一定唯一）。

举一个栗子：
给定一个无环有向图

按照图中数字123456789的顺序遍历，假如每访问一个点就把这个点删除掉，就会发现每次将要访问的那个节点必然无前驱（入度为0），此图除了123456789我们还能找出其他的拓扑序列：132645789、136247589….

宽搜的一个经典应用就是拓扑排序，一个 有向无环图(拓扑图) 必然存在拓扑排序（即它至少存在一个入度为0的点），无向图或者一个有环的图必然不存在拓扑排序。

思路
模拟我们上面提到过的，每访问完一个入度为0的节点就删除它，然后继续找入度为0的点访问，删除，不断重复（拓扑图必然存在入度为0的点），结束时，访问的路径就是拓扑序列。

1. 可以想像，所有入度为0的点都可以作为拓扑排序的起点，我们要做的第一件事就是把所有入度为0的点全部入队。
2. 弹出队列的队头元素（先把它保存到拓扑序列中），遍历其所有儿子，每访问一个儿子，就将该儿子的入度-1（切断它与它父亲的联系），然后判断：该儿子的入度是否为0？如果为0，说明下次能把它加入到拓扑序列中，现在把它push到队列中即可。这样保证了无论何时队列中任一节点入度总是为0，重复2的操作直到访问完毕，随之也得到了一个拓扑序列。

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N = 1e5+10;
int n, m;
int h[N], e[N], ne[N], idx; //邻接表
int d[N];       //存节点的入度
queue<int> q;   
vector<int> topo; //存储拓扑序列

void add(int a, int b) //增加一条边a->b
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
    d[b]++;
}

/*生成图的拓扑序列，失败返回0*/
bool TopSort()
{
    for(int i = 1;i<=n;i++) if(d[i]==0) q.push(i); //先把所有入度为0的点入队
    while(!q.empty())
    {
        int fore = q.front(); //取出一个入度为0的节点，保存在fore中
        topo.push_back(fore); //每次取队头的过程也是拓扑序列形成的过程
        q.pop();              //删除节点
        
        for(int i = h[fore]; i!=-1; i=ne[i]) //遍历fore的所有儿子
        {
            int succ = e[i];
            d[succ]--;         //把儿子的入度-1，切断与其父亲的联系
            
            /*
            如果这时儿子的入度为0了，它就被选中成为当前拓扑序列的下一
            个元素，将成为爸爸，因此将其压入队列。这样保证了该队列中的
            元素在任一时刻全是入度为0的点
            */
            if(d[succ]==0) q.push(succ); 
        }
    }
    return topo.size()==n; //如果生成的拓扑序列大小=总节点数，说明成功了
}

int main()
{
    memset(h, -1, sizeof(h));
    scanf("%d%d",&n,&m);
    int a,b;
    for(int i = 0;i<m;i++)
    {
        scanf("%d%d",&a,&b);
        add(a, b);
    }
    if(!TopSort())
    {
        printf("-1\n");
        return 0;
    }
    for(int i = 0;i<topo.size();i++) printf("%d ", topo[i]);
    return 0;
}

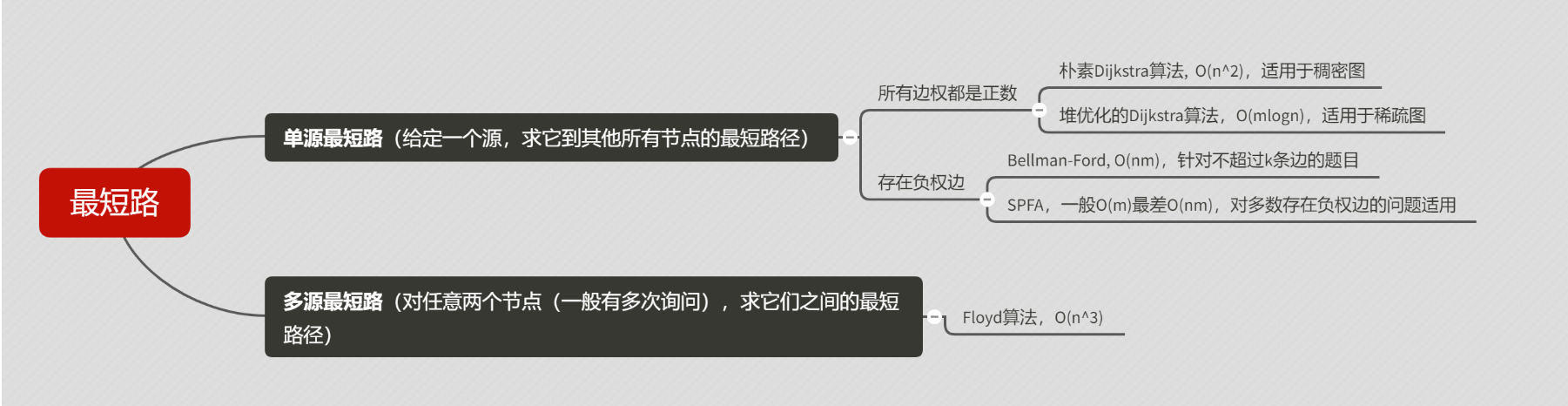
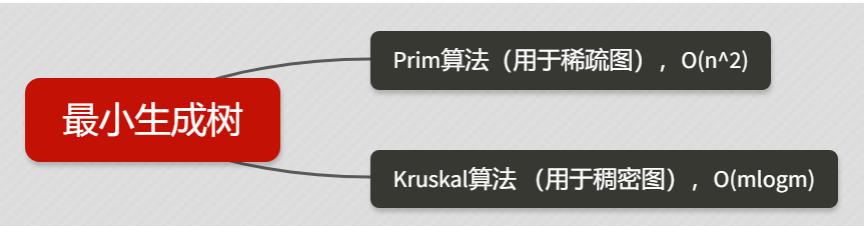
3. 最短路问题

在不同的情境下有不同的最短路算法，假定n为节点数，m为边数：

如何区分稠密图和稀疏图？
如果边数与节点数差不多，就是稀疏图；
如果边数比节点数多很多，就是稠密图。

最短路问题最大的难点在于如何把问题抽象成最短路问题，即如何定义节点和边

3.1 普通Dijkstra算法

专用于稠密图，用邻接矩阵存储。

思路:

1. 每次都在所有还未确定最短路径的顶点中，选出一个与起点距离最近的顶点t，那么可以确定，目前记录的起点到顶点t的距离就是它们的最短距离。
2. 确定了顶点t的最短路径后，以它与起点之间的距离为基础，更新它所有后继到起点的距离。
3. 重复上述动作，直到确定所有顶点的最短路径为止。

题目：给定顶点数n和边数m，求顶点1到顶点n的最短距离。

#include<iostream>
#include<cstring>
using namespace std;
const int N = 510;

int n, m;       //用户输入的顶点数和边数
int g[N][N];    //本题为稠密图，选择用邻接矩阵来表示
int st[N];      //起点到某个顶点i的最短路径是否已经确定
int dist[N];    //起点到某个顶点i【目前的】最短距离

/*返回顶点1到顶点n的最短距离，返回-1表示无法到达*/
int dijkstra()
{
    memset(dist, 0x3f, sizeof(dist)); //将起点到所有其余顶点的距离初始化为无穷大
    dist[1] = 0; //起点到它自己的距离为0
    
    for(int i = 0;i<n;i++)//寻找起点到所有其余顶点的最短距离
    {
        int t = -1;
        for(int j = 1;j<=n;j++) //在所有【没确定最短路径但与起点距离已知的顶点中】选择一个与起点距离【最近】的顶点t
        {
            if(!st[j] && (t==-1 || dist[t] > dist[j])) t = j;
        }
        
        st[t] = true; //对于上一步找到的顶点t，它的dist[t]可以被确定为【到起点的最短距离】
        
        for(int j = 1;j<=n;j++)//更新顶点t所有【出边】到起点的最短距离
        {
            dist[j] = min(dist[j], dist[t] + g[t][j]);
        }
        
    }
    
    if(dist[n]==0x3f3f3f3f) return -1; //图中某一个顶点无法到达
    return dist[n]; //若能到达，返回起点到终点的最短距离
}

int main()
{
    scanf("%d%d",&n,&m);
    memset(g, 0x3f, sizeof(g)); //图中所有不存在的边全部定义为无穷大
    
    int x,y,z;
    for(int i = 0;i<m;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        g[x][y] = min(g[x][y], z); //因为存在重边，我们只保留距离最短的边
    }
    printf("%d\n",dijkstra());
    return 0;
}

3.2 堆优化版Dijkstra算法

专用于稀疏图，用邻接表存储。
思路: 朴素Dijkstra有一个步骤非常慢：从所有未确定最短路的顶点中找出距离起点最近的那一个，时间复杂度为O(n^2)。对于这样多次询问最大最小值的问题，用堆来实现会快的多。

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N = 1000010;
typedef pair<int, int> PII; /*堆的元素类型，first为distance， second为顶点编号，STL堆默认按第一个元素排序*/

int e[N], ne[N], h[N], w[N], idx; //稀疏图，用邻接表存储
int dist[N];    //顶点i到起点的【目前的】最短距离
int st[N];      //顶点i到起点的最短距离已经得出
int n, m;       //用户输入的顶点数和边数


void add(int a, int b, int c)
{
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx++;
}

/*返回顶点1~n的最短距离，无法到达则返回-1*/
int Dijkstra()
{
    memset(dist, 0x3f, sizeof(dist)); //将所有其他顶点与起点的距离初始化为无穷大
    dist[1] = 0; //起点与它自己的距离为1
    priority_queue<PII, vector<PII>, greater<PII>> heap; //创建小根堆
    heap.push({0, 1});  //往堆中push起点的信息，1号节点距离自己的距离为0
    
    while(!heap.empty()) //遍历所有顶点
    {
        PII fore = heap.top(); //取出所有顶点中距离起点最近的那一个
        heap.pop();
        
        int distance = fore.first; //拿到该顶点与起点的距离，它就是该顶点与起点的【最短距离】
        int ver = fore.second;     //拿到该顶点的编号
        
        if(st[ver]) continue;      //如果该顶点的最短路径之前就已经被确定了，就不用管这个点
        
        /*从fore这个已经确定最短路径的顶点出发，更新它所有后继的最短距离*/
        for(int i = h[ver]; i!=-1; i = ne[i]) 
        {
            int succ = e[i];  //取出顶点编号
            
            if(distance + w[i] < dist[succ]) //w[i]是fore与其任意后继i的边权
            {
                dist[succ] = distance + w[i];
                heap.push({dist[succ], succ}); //把更新写入到堆中
            }
        }
        
        st[ver] = true;            //将fore顶点标记为已确定最短路径
    }
    
    if(dist[n]==0x3f3f3f3f) return -1; //无法到达
    return dist[n]; //返回顶点1~n的最短距离
}

int main()
{
    scanf("%d%d",&n,&m);
    memset(h, -1, sizeof(h));
    int a, b, c;
    for(int i = 0;i<m;i++)
    {
        scanf("%d%d%d",&a,&b,&c);
        add(a, b, c);
    }
    printf("%d\n",Dijkstra());
    return 0;
}

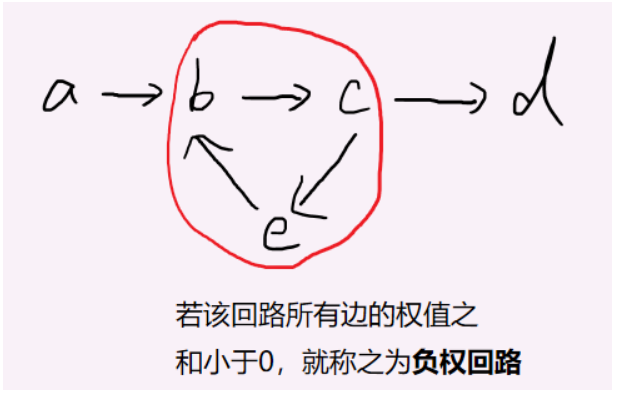
3.3 Bellman-Ford算法

针对于存在负权边的（且限制了最多走k条边的）最短路问题，要注意的是图中如果存在负权回路，那么最短路可能不存在。

负权回路是指：

Bellman-Ford算法十分的暴力，它的策略如下：

1. 将起点外所有点的距离初始化为无穷大，起点距离为0。
2. 起点到终点最多允许经过k条路（一般有此限制才使用bellman-ford算法），因此总共要循环k次找路（每次确定一条边）。每次找路都会遍历所有边，如果该边的前驱与起点的距离不是无穷大（即其前驱被更新过）：
   a. 则该利用其前驱来更新自己的后继到起点的距离；
   b. 或者该边的后继本身已经被更新过了（与起点的距离不是无穷大），这次可能利用其前驱更新一条更短的一条路。

该算法设计时有一些小细节，举例如下：
题目：只允许走一条边找最短路。

因为我们的算法中，每次确定一条边都要遍历所有边，这样就会产生一些问题。
比如在本例确定第一条边，遍历所有边的过程中，先遍历到第一条边，其前驱起点1到起点的距离为0，不为无穷大，就用它来更新其后继顶点2到起点的距离（为1），那么这时用于保存起点到某顶点距离的dist数组中，dist[2]就会从无穷大更新为1。
接着，我们遍历到第二条边，前驱为2后继为3，因为我们的算法是否更新当前边的后继到起点的距离完全是依据它的前驱是否已经被更新过（即其前驱到起点的距离是否为无穷大），本例此时第二条边的后继顶点3就会依据其前驱到起点的距离dist[2]的值是否为无穷大来决定是否更新，发现dist[2]不为无穷大，因此后继顶点3就会根据前驱顶点2来更新到起点的距离（dist[3]=2），最后返回最短路径2，这就不对了。我们的算法本意是要一条边一条边的确定，上述情况却一次确定了两条边，但它还以为只确定了一条。
为了防止出现这种情况，在本轮找边，遍历每一条边时，其前驱都使用上一轮找边结束时所有顶点的状态即可，反映到代码上就是每轮找边开始时把dist数组复制到backup数组中，之后使用的前驱都从backup数组中取。

例题: 存在负环的图中，经过不超过k条边从起点到顶点n的最短路径长度。

#include<iostream>
#include<cstring>
using namespace std;
const int N = 100010;
const int M = 10010;
int n, m, k; //用户输入的顶点数，边数和最短路允许经过的最大边数
struct Edge //用最原始的方法表示图
{
    int a; //前驱
    int b; //后继
    int w; //边权
}edge[M];

int dist[M], backup[M]; //backup保存上一轮找边后dist数组的状态

int BellmanFord()
{
    //初始化
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;
    
    for(int i = 0;i<k;i++) //限制从1到n最多允许经过k条边
    {
        memcpy(backup, dist, sizeof(dist)); //保存上一轮结束时dist数组的状态
        for(int j = 1;j<=m;j++) //遍历所有边
        {
            Edge e = edge[j]; 
            dist[e.b] = min(dist[e.b], backup[e.a] + e.w); //根据当前边的前驱来更新其后继
        }
    }
    /*
    因为存在负权边，无穷大之间也可能相互更新
    距离，因此不能用dist[n]==0x3f3f3f3f来判断。
    */
    if(dist[n] > 0x3f3f3f3f/2) return -1; 
    
    return dist[n];
}

int main()
{
    scanf("%d%d%d",&n, &m, &k);
    for(int i = 1;i<=m;i++)
    {
        scanf("%d%d%d", &edge[i].a, &edge[i].b, &edge[i].w);
    }
    int re = BellmanFord();
    if(re==-1) printf("impossible");
    else printf("%d\n",dist[n]);
    
    return 0;
}

3.4 SPFA

本质上是对bellman-ford算法的优化。
SPFA在非稠密图中的时间复杂度比较低，在负权图中是比较优先的选择，虽然在纯正权图中有时也可以使用SPFA快速解出，但是不稳定，因此纯正权图中还是老老实实的用Dijkstra。

回忆bellman-ford算法，它之所以暴力的原因在于，每找一条边都要遍历所有的边，而大多数遍历其实是在做无用功（比如一开始，只有起点距离起点的距离已知，那么这一轮只能更新起点的所有后继，其他的遍历都是浪费）。
我们可以用邻接表来存储图，然后用一个队列（或其他结构，只要能保存顶点即可）来优化belman-ford算法（类似于广搜），所有其后继需要被更新的顶点会被放在队列中，一开始只有起点在队列中，在遍历所有队列中顶点的后继时，只有当某一个顶点的距离被更新后，才会将它入队，才会在之后更新它的所有后继，因为一个顶点的路径更新了会影响到它所有的后继；而如果遍历到的某顶点无法被更新（要么新路径还没有旧路径短，要么该顶点的前驱与起点的距离还处于未知状态），就会跳过它，暂时不对它的后继做任何测试。这样一来，每一次遍历都是有意义的了，相比bellman-ford节省了很多时间。

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N = 100010;
int n, m; //用户输入的顶点数和边数

/*w[i]表示当前顶点到其地址为i的后继的边权，因为遍历
邻接表每次都是固定一个前驱，遍历其所有后继，因此只需
要一个后继的地址就能确定一条边*/
int h[N], ne[N], e[N], dist[N], w[N], idx; 
bool st[N]; //某顶点是否已存在队列中
void add(int a, int b, int c)
{
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx++;
}

int spfa()
{
    dist[1] = 0;
    queue<int> q; //如果某个点的距离被更新了，就放入队列中，之后还要对其后继进行更新
    q.push(1); //先将起点放入队列
    st[1] = true;  //将起点标记为已存在队列中
    
    while(!q.empty())
    {
        int fore = q.front(); 
        q.pop();
        
        st[fore] = false; //顶点fore被从队列中pop出来了，将其标识为不存在队列中
        
        for(int i = h[fore]; i!=-1; i = ne[i]) //遍历fore的所有后继
        {
            int succ = e[i]; //获取后继顶点的编号
            
            /*如果新路比老路还远，就跳过，去检查下一个后继顶点能否被
            更新。否则新路比老路要近，进入条件*/
            if(dist[succ] > dist[fore]+w[i])  
            {
                dist[succ] = dist[fore]+w[i]; //立即放弃老路，选择新路
                
                /*顶点succ的距离被更新了，那么它所有后继的距离也都应该改变，因此要
                把它存入队列，在之后更新它的所有后继。而如果succ这个顶点已经存在队列
                中，就不用重复放入了*/
                if(!st[succ]) 
                {
                    st[succ] = true;
                    q.push(succ);
                }
            }
        }
    }
    if(dist[n]==0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    memset(h, -1, sizeof(h));
    memset(dist, 0x3f, sizeof(dist));
    scanf("%d%d",&n,&m);
    int a,b,c;
    for(int i = 0;i<m;i++)
    {
        scanf("%d%d%d",&a, &b, &c);
        add(a, b, c);
    }
    int re = spfa();
    if(re==-1) printf("impossible\n");
    else printf("%d\n",re);
    return 0;
}

3.4.1 SPFA判断是否存在负环

其方法就是在SPFA中的每一句:
dist[value] = dist[head] + w[i];
的后面加上一句
count[value] = count[head] + 1;
来计算当前每一条路径需要经过的边数，如果某一个count[value]≥n的话，就表示该图中存在负环。

另外需要注意的是，我们不能总是以编号为1的顶点出发寻找负环，因为有可能达到不了负环，所以我们要从每一个顶点出发，也就是最一开始要把所有的顶点全部push到队列中。那么在这样的条件下，我们也不需要把dist数组初始化为无穷大了，全部为0即可。

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;

const int N = 100010;
int e[N], ne[N], h[N], w[N], cnt[N], st[N], dist[N], idx;
int n,m; //用户输入的顶点数和边数
void add(int a, int b, int c)
{
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx++;
}

bool spfaJ()
{
    //不需要初始化dist数组，让它自然的全部为0即可，找到负边自然会更新
    
    queue<int> q;
    
    //如果从单个顶点开始，可能够不到负环，因此我们把从每个顶点开始都试一遍
    for(int i = 1;i<=n;i++) 
    {
        q.push(i);
        st[i] = true;
    }
    
    while(!q.empty())
    {
        int fore = q.front();
        q.pop();
        st[fore] = false;
        
        for(int i = h[fore]; i!=-1;i = ne[i])
        {
            int succ = e[i];
            if(dist[succ] > dist[fore]+w[i]) 
            {
                dist[succ] = dist[fore]+w[i];
                cnt[succ] = cnt[fore]+1;  //每次更新某顶点距离，都会记录起点到该顶点路径上所有的边数
                
                /*最短路最多只能经过n-1条边，如果某顶点与起
                点之间路径的边数大于等于n，那么一定存在负环*/
                if(cnt[succ]>=n) return true; 
                
                if(!st[succ])
                {
                    q.push(succ);
                    st[succ] = true;
                }
            }
        }
    }
    return false;
}

int main()
{
    memset(h, -1, sizeof(h));
    scanf("%d%d",&n,&m);
    int a,b,c;
    for(int i = 0;i<m;i++)
    {
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
    }
    int re = spfaJ();
    if(re) printf("Yes\n");
    else printf("No\n");
    return 0;
}

3.5 Floyd算法

使用该算法的前提是图中没有负权回路，且由于该算法的复杂度为O(n^3)，因此图的顶点数必须限制在200以内，所以在使用该算法时我们可以总是用邻接矩阵来存图。

该算法的思路：
要求任意顶点i到j之间的最短路。
首先将顶点1视为中转点，判断i→1→j是否比原本i→j的路程要短，如果短则更新，再将顶点2视为中转点，判断i→2→j是否比原本i→j的路程短，短则更新，再将顶点3视为中转点….
直到把最后一个顶点视为中转点，更新完i→j的最短路后，邻接矩阵中任意一个坐标(i, j)中的值就是顶点i→j的最短路了。

题目：给定一个无负权环的图，顶点数不超过200，Q次询问任意两点之间的最短路长度。

#include<iostream>
#include<cstring>
using namespace std;
const int N = 210; //顶点数不能超过200
const int INF= 0x3f3f3f3f;
int n,m,Q; //用户输入的顶点数，边数，和询问两点间最短路径的次数
int g[N][N];

void floyd()
{
    for(int k = 1; k<=n; k++) //枚举所有顶点作为中转点
    {
        for(int i = 1;i<=n;i++) //起点
        {
            for(int j = 1; j<=n;j++) //终点
            {
                /*以k为中转点时，如果i→k→j的距离比原本i→j的距离短，则更新*/
                g[i][j] = min(g[i][j], g[i][k]+g[k][j]);
            }
        }
    }
}



int main()
{
    scanf("%d%d%d",&n,&m,&Q);
    for(int i = 1;i<=n;i++) //初始化邻接矩阵
    {
        for(int j = 1;j<=n;j++)
        {
            if(i==j) g[i][j] = 0; //顶点到自己的距离为0
            else g[i][j] = INF;   //到其他顶点的距离初始化为无穷大
        }
    }
    
    int x, y, z;
    for(int i = 0;i<m;i++) //将数据读入邻接矩阵
    {
        scanf("%d%d%d",&x, &y, &z);
        g[x][y] = min(g[x][y], z);
    }
    
    floyd();  //用floyd算法将邻接矩阵更新为最短路邻接矩阵
    
    for(int i = 0;i<Q;i++) //Q次询问x→y的最短路距离
    {
        scanf("%d%d", &x, &y);
        int re = g[x][y];
        
        /*判断【re>INF/2】是因为存在无穷大之间互相更新
        的情况，即有些顶点的距离【是】无穷大，但这个无穷大
        的值并不严格等于INF=0x3f3f3f3f*/
        if(re>INF/2) printf("impossible\n"); 
        else printf("%d\n", re);
    }
    return 0;
}

4. 最小生成树

最小生成树的任务：在不产生回路的情况下，以最短的路径连通一张图的所有顶点。
最小生成树的定义：用带权无向连通图生成的树，它无环地包含了这张图中所有的顶点，且它所有的边都是图中的边。在所有满足这样条件的树当中，边权总和最小的就是最小生成树。

4.1 Prim算法

prim算法思路：
定义一个连通块，一开始块中只有起点，接着每一步都找一个距离连通块最近的顶点，将其合并到顶点中，直到所有顶点都被合并到连通块中后，该连通块就形成了一颗最小生成树。

从起点开始，更新它所有的后继的距离，再在已经被更新过距离的所有顶点（目前为起点的所有后继）中找到一个与起点（初始时的连通块）距离最近的顶点作为t，将其加入连通块；然后更新t的所有后继，再在已经被更新过距离的所有顶点中找到一个距离连通块最近的点作为t，将其加入连通块，然后更新t的所有后继…..
直到每一个顶点都被加入连通块后，最小生成树就是这个连通块。

prim算法与Dijkstra的区别也在连通块，dist数组在prime算法中并不表示某个顶点到起点的最短距离，而是表示某个顶点到当前连通块的最小距离。

不太明白的话照着代码模拟一遍就懂了。

【题目】

https://www.acwing.com/problem/content/860/

在一个存在重边和自环的无向图（存在负权边）中找出最小生成树

#include<iostream>
#include<cstring>
using namespace std;
const int N = 510;
const int INF = 0x3f3f3f3f;
int g[N][N];
int st[N]; //记录某顶点是否在连通块中
int dist[N]; //记录顶点i到连通块的最短距离
int n, m; //用户输入的顶点数和边数

int prim()
{
    memset(dist, 0x3f, sizeof(dist));
    int sum = 0;        //最小生成树的总边权
    for(int i = 0; i<n;i++)
    {
        int t = -1;
        
        //在所有连通块之外且距离被更新过的顶点中，找一个与连通块距离最近的顶点
        for(int j = 1; j<=n;j++) 
        {
            if(!st[j] && (t==-1 || dist[t] > dist[j])) t = j;
        }
        
        //如果除起点外任一顶点与连通块的距离为无穷大，则表示图不连通， 故不存在最小生成树
        if(i && dist[t]==INF) return -1; 
        
        /*每次找到的【距离连通块最近的】顶点t，它会被同化
        到连通块中，作为最小生成树中的一个节点，并且它
        与连通块相连的边也作为最小生成树中的一个边*/
        if(i) sum+=dist[t]; 
        
        st[t] = true; //顶点t加入到连通块中
        
        for(int j = 1;j<=n;j++) //更新t所有后继与【t】(可理解成连通块)的距离
        {
            dist[j] = min(dist[j], g[t][j]);
        }
        
        
    }
    return sum;
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i = 1;i<=n;i++) //初始化邻接矩阵
    {
        for(int j = 1; j<=n;j++)
        {
            if(i==j) g[i][j] = 0;
            else g[i][j] = INF;
        }
    }
    int x,y,z;
    for(int i = 0;i<m;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        g[y][x] = g[x][y] = min(g[x][y], z); //无向图所以一条边要添加两个方向
    }
    int re = prim();
    if(re==-1) printf("impossible\n");
    else printf("%d\n",re);
    return 0;
}

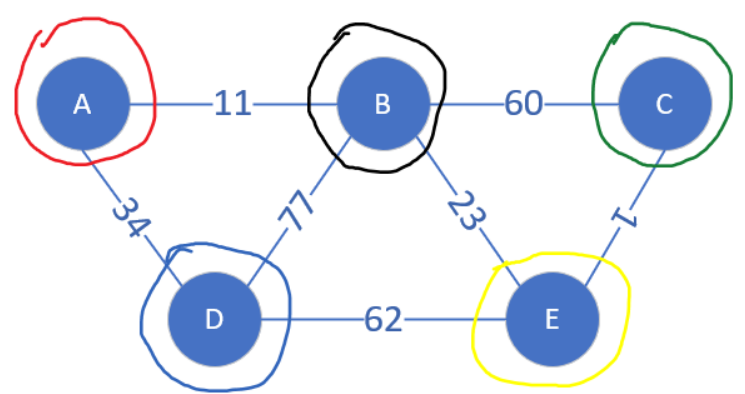
4.2 Kruskal算法

Kruskal算法策略如下：

下面来模拟，不同颜色的圈代表不同连通块

排序后遍历所有的边，先走到CE边，它的两个顶点分属不同的连通块，将它们合并。

接下来找到AB边，其两个顶点分属不同的连通块，合并。

接下来是BE边，B和E属于不同连通块，合并。

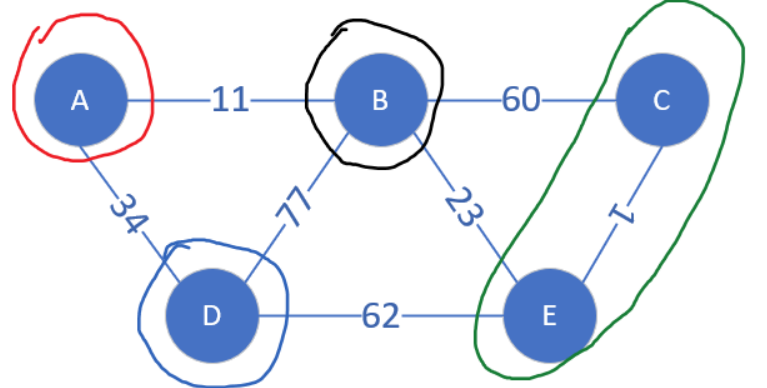
假如现在连通块之外最小的边是BC，顶点B和C属于同一个连通块，这条边就会被跳过。否则如果合并就会产生回路了。
不过现在的情况是连通块外最小的边是AD，它们不属于同一个连通块，合并它们。

现在连通块中边的数量等于顶点总数-1，说明最小生成树已经被找到了。把点逐渐合并为连通块的工作，我们可以借助并查集来完成。

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e5+10;
int p[N]; //并查集
int n,m; //用户输入的顶点数和边数

struct Edge
{
    int a; //前驱
    int b; //后继
    int w; //权值
}edge[N*2];

int cmp(Edge x1, Edge x2) //Edge之间以边权来比较大小
{
    return x1.w<x2.w;
}

//带路径压缩的并查集查找
int find(int x)
{
    if(p[x]!=x) p[x] = find(p[x]);
    return p[x];
}

int kruskal()
{
    int sum = 0; //生成树的总边权
    int cnt = 0; //目前生成树的总边数
    
    sort(edge, edge+m, cmp); //把所有边按权值从小到大排序
    
    for(int i = 1;i<=n;i++) p[i] = i; //初始化并查集
    
    //遍历所有排好序的边
    for(int i = 0;i<m;i++) 
    {
        int a = edge[i].a;
        int b = edge[i].b;
        int w = edge[i].w;
        
        int root1 = find(a);
        int root2 = find(b);
        if(root1!=root2) //如果两个顶点的标记不同
        {
            p[root1] = root2; //就把这两个顶点所属的连通块合并
            sum+=w; //更新当前生成树的总边权
            cnt++; //更新当前生成树的总边数
        }
        
        /*因为最小生成树是无环的并且连接了图中所有的顶点，因此当
        生成树中的边数为顶点数-1时就代表已经找到正确的最小生成树*/
        if(cnt==n-1) return sum; 
    }
    
    return -1;
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i = 0;i<m;i++)
    {
        scanf("%d%d%d",&edge[i].a,&edge[i].b,&edge[i].w);
    }
    int re = kruskal();
    if(re==-1) printf("impossible\n");
    else printf("%d\n",re);
    return 0;
}

5. 二分图

二分图定义：可以把图中所有顶点分割为两个互不相交的子集，每一条边对应的两个顶点都分属于不同的子集。
类似于这样

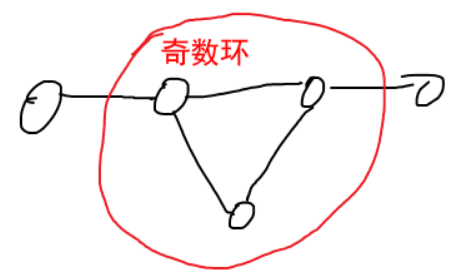
再介绍一个概念奇数环：边数为奇数的环

二分图还可以这样定义：所有不含有奇数环的图都是二分图

使用染色法可以判断一个图是否为二分图。

5.1 染色法判断二分图

染色法判断一个图是否为二分图，时间复杂度O(V+E)。

思路：遍历所有顶点（因为图可能不连通），对每一个顶点，将它所属的连通块全部染色。
染色方法：先定义好起始顶点的颜色，然后遍历它的后继并将它们颜色涂为与它们的前驱相反的颜色，然后再遍历后继的后继….直到该连通块全部染色完毕。在染色中途如果检查到某个顶点和它的前驱颜色相同，则返回false，表明该图不是二分图。

5.1.1 DFS实现

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;
const int N = 1e5 + 10, M = 2e5 + 10;


int e[M], ne[M], h[N], idx;
int n, m; //用户定义的顶点数和边数
int colored[N]; //表示某个顶点的颜色状态，0表示无颜色，1和-1表示相反的颜色

void add(int a, int b){
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}


/*把顶点v所属的连通块全部染色*/
bool DfsColoring(int v, int color){
    colored[v] = color;             //先给起点选定一种颜色
    for(int i = h[v]; i!=-1;i = ne[i]) //遍历v所属的整个连通块
    {
        int succ = e[i];   //获取e[i]的后继succ
        if(!colored[succ]) //如果succ还没有被染色
        {
            //就以深度优先的方式给它染上与e[i]相反的颜色
            if(!dfs(succ, ~color)) return false; 
        }
        //如果染色过程中某个顶点与其前驱的颜色相同，就表示该图不是二分图
        else if(colored[succ]==color) return false; 
    }
    return true; //顶点v所属连通块染色完毕
}

int main(){
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);
    while(m --){
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a); // 无向图
    }

    int flag = true;
    
     //因为图可能不连通，所以要对所有顶点所属连通块进行染色
    for(int i = 1; i <= n; i ++) {
        if (!colored[i]){ //如果该顶点所属连通块还没被染过色
        
            /*就假定起点的颜色为1，对它所属的整个
            连通块染色。如果在染色的过程中出现相邻
            顶点颜色相同的情况，说明该图不是二分图*/
            if(!DfsColoring(i, 1)){ 
                flag = false;
                break;
            }
        }
    }

    if (flag) puts("Yes");
    else puts("No");
    return 0;
}

5.1.2 BFS实现

#include <iostream>
#include <algorithm>
#include <queue>
#include <cstring>

using namespace std;
const int N = 1e5 + 10, M = 2e5 + 10;


int e[M], ne[M], h[N], idx;
int n, m; //用户定义的顶点数和边数
int colored[N]; //表示某个顶点的颜色状态，0表示无颜色，1和-1表示相反的颜色

void add(int a, int b){
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}


/*把顶点v所属的连通块全部染色*/
bool BfsColoring(int v, int color){
    queue<int> q;
    q.push(v);
    colored[v] = color;             //先给起点选定一种颜色
    
    while(!q.empty())
    {
        int fore = q.front();
        q.pop();
        
        for(int i = h[fore]; i!=-1;i=ne[i]) //遍历fore的所有后继
        {
            int succ = e[i];
            if(!colored[succ])  //给无颜色的顶点succ染色
            {
                colored[succ] = ~colored[fore];
                q.push(succ);
            }
            else if(colored[succ]==colored[fore]) return false; //如果后继和前驱颜色相同，则不是二分图
            else continue;
        }
    }
    
    return true;
}

int main(){
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);
    while(m --){
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a); // 无向图
    }

    int flag = true;
    
     //因为图可能不连通，所以要对所有顶点所属连通块进行染色
    for(int i = 1; i <= n; i ++) {
        if (!colored[i]){ //如果该顶点所属连通块还没被染过色
        
            /*就假定起点的颜色为1，对它所属的整个
            连通块染色。如果在染色的过程中出现相邻
            顶点颜色相同的情况，说明该图不是二分图*/
            if(!BfsColoring(i, 1)){ 
                flag = false;
                break;
            }
        }
    }

    if (flag) puts("Yes");
    else puts("No");
    return 0;
}

5.2 匈牙利算法

理论时间复杂度O(VE)，实际一般远低于VE。
也可称为二分图最大匹配算法（媒婆算法），首先要介绍几个概念。
匹配：二分图两侧某一对顶点被唯一的一条边相连

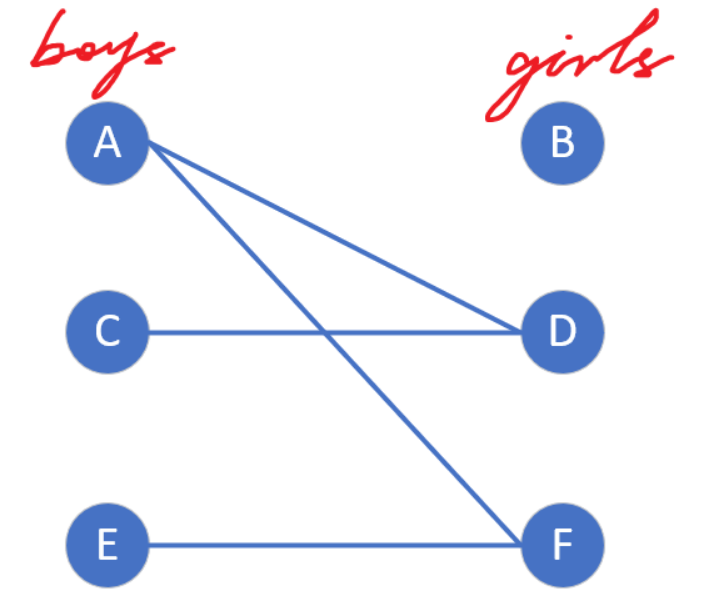
例如这样的一张二分图

我们把它视为适婚年龄男女的恋爱关系图，左侧男生，右侧女生，连线表示互相有好感，现在从媒婆的角度来介绍匈牙利算法实现过程（让最多对男女牵线成功），传授给读者一些人生经验。

遍历左侧所有顶点（男生）：

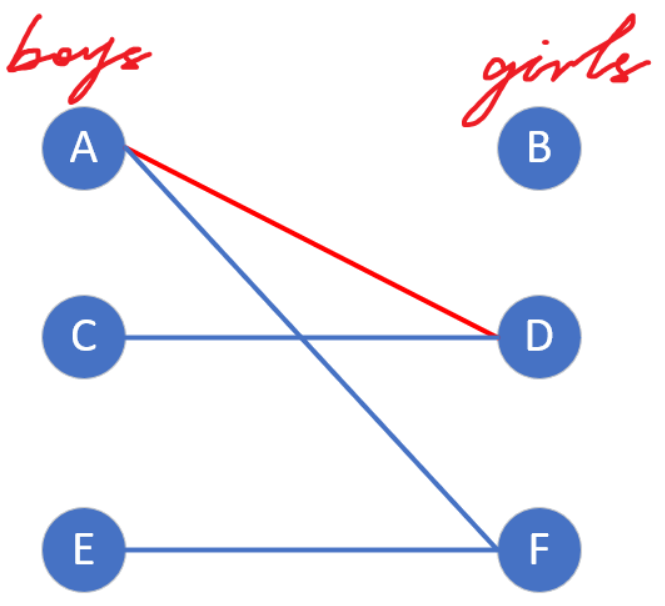
A的第一个喜欢的女生是D，发现D还没有被匹配，就直接与它匹配，它们开始约会。

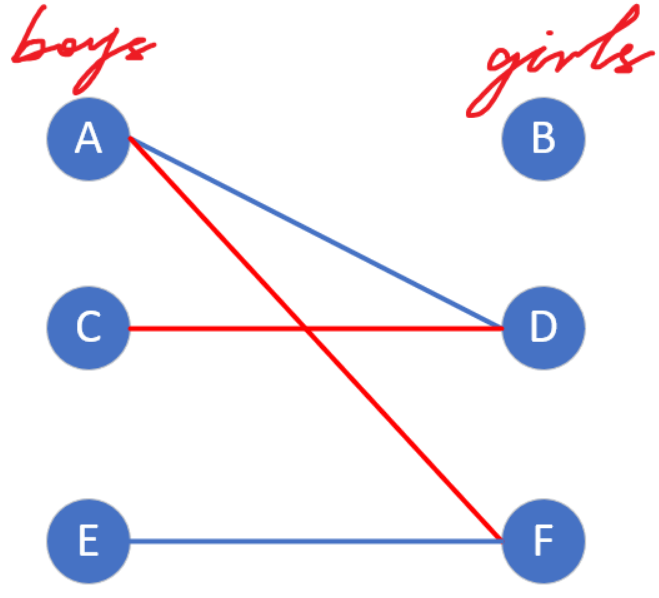
A匹配完成，开始与D约会。现在要为下一个男生C牵线搭桥，C第一个喜欢的女生是D，而D已经与A匹配了，这时怎么办呢？C会直接对D表白，我想要与你约会，如果你现在有男朋友，就看看你的现男友有没有其他喜欢的女生，让他换一个对象；如果没有，现在就跟我处对象。

当天晚上，D就会去告诉A：”你如果有其他喜欢的女生，就去尝试跟她匹配吧，如果匹配上了，就忘了俺，俺去跟C好了，如果你实在找不到，那俺也不会抛弃你，继续跟你好。

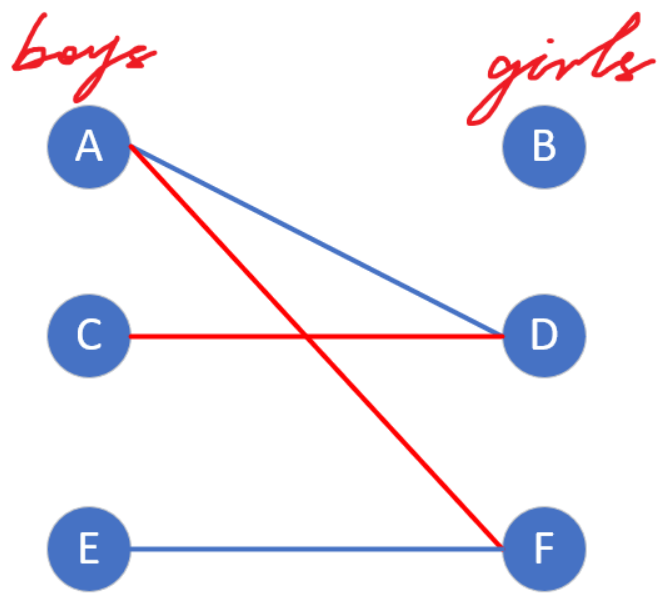
A也不生气，因为他已看破红尘，D这样坦诚对双方都有好处。接着他就去找他其他的暗恋对象，发现F没有匹配，于是乎，皆大欢喜。

现在A和C都已经找到对象了，小E也准备着去跟暗恋多年的对象F告白了。
订好了饭店，准备了花束，好不容易把F约出来，在饭局的尾声鼓足了勇气对F深情告白，没想到答案却是：“你是个好人，不过我现在已经在跟A约会了，我先回家洗澡了，再见。”
百感交集的E气的嗷嗷叫，立马杀到A家门口，开出500万的价格让他离开小F。A寻思了一会，手中把玩着劳斯莱斯幻影的车钥匙，拒绝了E的要求。
因此最后的关系图得到了。

#include<iostream>
#include<cstring>
using namespace std;

const int N = 510;
const int M = 1e5+10;
int n1, n2, m; //用户输入的男生数，女生数，和边数
int h[N], ne[M], e[M], idx;


int matched[N]; //matched[i]=a表示女生i目前与男生a约会中
bool callDibs[N]; //callDibs[i]表示女生i是否已经被告白

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

/*尝试为男生x找一个女朋友*/
bool find(int x)
{
    for(int i = h[x]; i!=-1; i = ne[i]) //遍历男生x暗恋的所有女生
    {
        int succ = e[i];  
        
        if(!callDibs[succ]) //如果当前女生没有被任何男生告白
        {
            callDibs[succ] = true; //那么现在她就要被x告白了
            
            /*如果这个女生现在没有男朋友，或者她有男
            朋友，但她男朋友愿意换一个女生交往*/
            if(!matched[succ] || find(matched[succ])) 
            {
                matched[succ] = x; //那么x就可以直接开始与当前女生约会了，匹配成功
                return true;
            }
        }
    }
    return false; //如果男生x暗恋的所有女生都有男友，且她们的男友都不愿意换女友，则x单身
}

int main()
{
    memset(h, -1, sizeof(h));
    scanf("%d%d%d",&n1, &n2, &m);
    int x, y;
    for(int i = 0;i<m;i++)
    {
        scanf("%d%d",&x ,&y);
        add(x, y);
    }
    int res = 0; //最多匹配成功多少对情侣
    for(int i = 1; i<=n1;i++) //帮所有男生（二分图左侧所有顶点）找女朋友
    {
        /*每【尝试完】为一个男生匹配一个女生，匹配过
        程中他对其他女生的表白记录就已经无效了。因
        此在为下一个男生牵线搭桥之前，要先清空上一个男
        生的表白记录*/
        memset(callDibs, 0, sizeof(callDibs)); 
        if(find(i)) res++;
    }
    printf("%d\n", res);
    return 0;
}