《堆》专题

Posted on Edited on In , Views:

关于堆的算法。

堆是一颗完全二叉树，它具有这样的性质（以小根堆为例）：父节点的值永远小于等于其左右孩子，大根堆则反之, 这样的结构使得我们可以在O(1)的时间内找到数组的最值。
因为它本身是完全二叉树，所以可以用一个一维数组来表示，按层序给每个节点标号（从1开始），则某节点x的左儿子=2x，右儿子是2x+1.

堆有两个基础操作：up和down，所有其他的操作都可以用这俩拼出来。

1. 基本模板

1.1 down操作

down(x)，就是在节点x的左右子树（不包括x）均满足堆的定义的情况下，加入x节点，使得x及其左右子树均满足堆的定义。
假定一个完全二叉树（除了根其余部分都满足堆性质，节点编号从1开始）

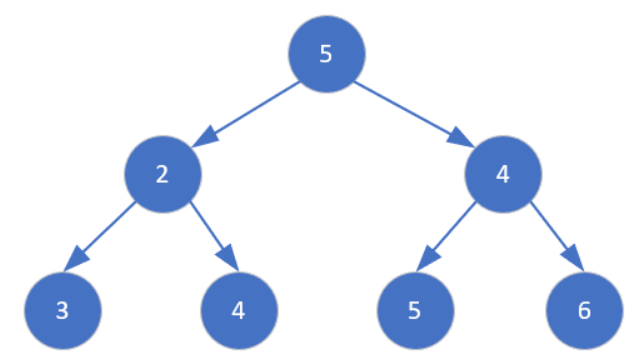
在节点1的左右子树均满足堆的定义的前提下，执行down(1)，则一号节点5会与其左右子节点2、4比较，发现它们三个的最小值是2，为了使其满足堆的性质，交换2和5的位置。

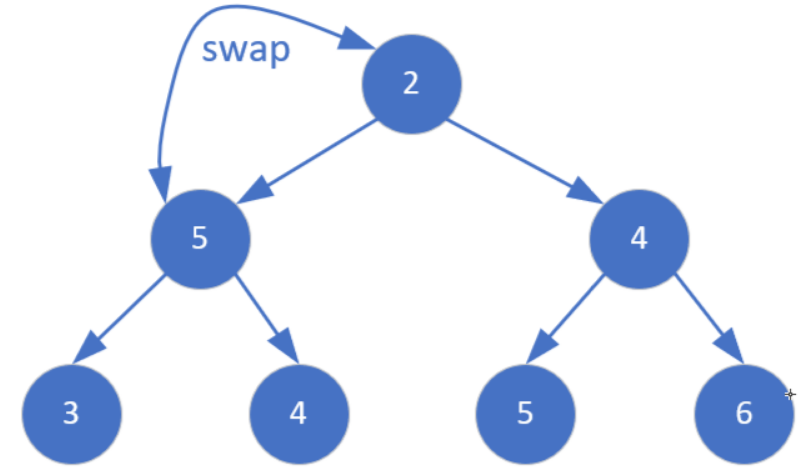
交换后，5与其现在的左右子节点又不满足堆的性质了（5比3和4都大），所以又要以二号节点5为父节点，重复上述步骤，即down(2)。

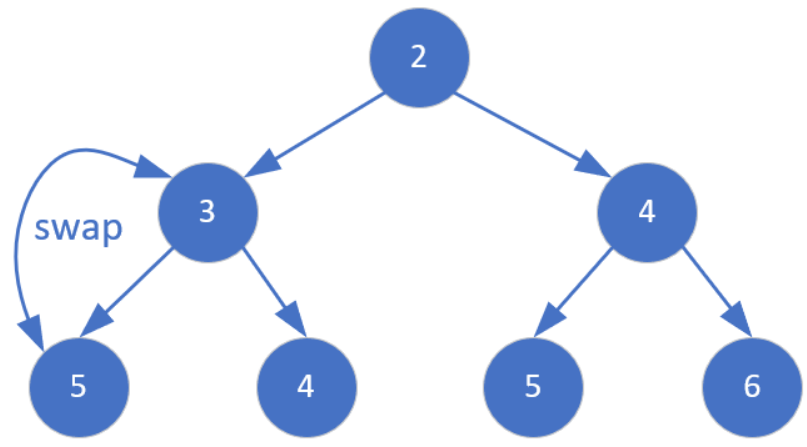
这样我们就完成了down操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int size；//当前节点数量
int h[]; //用来表示堆的数组

void down(int x) //从标号为x的结点开始往下一路“堆化”
{
    int min = x;//准备寻找三个节点中的最小节点
    //如果x的左儿子存在，且小于x， 则将它标注为最小节点
    if(x*2 <= size && h[x*2]<h[min]) min = x*2;
    //如果x的右儿子存在，且小于x，则将他标注为最小节点
    if(x*2+1<=size && h[x*2+1]<h[min]) min = x*2+1;
    if(x!=min) //如果x不是最小的
    {
        swap(h[x], h[min]); //就交换x和最小节点的位置
        down(min); //因为x不是最小的，所以min所在位置必定是x的子节点，在它们交换后，min位置的元素变了，因此我们要以min为父节点继续检查它与其左右子树是否满足堆结构。
     }
 }

有了down方法后，我们可以非常方便的将数组转化为堆。

1.2 快速将数组转化为堆

1
for (int i = n / 2; i; i -- ) down(i);

n为数组的size，在完全二叉树中，n/2代表非叶节点的个数，为啥从n/2开始往上down就能转化成堆呢？

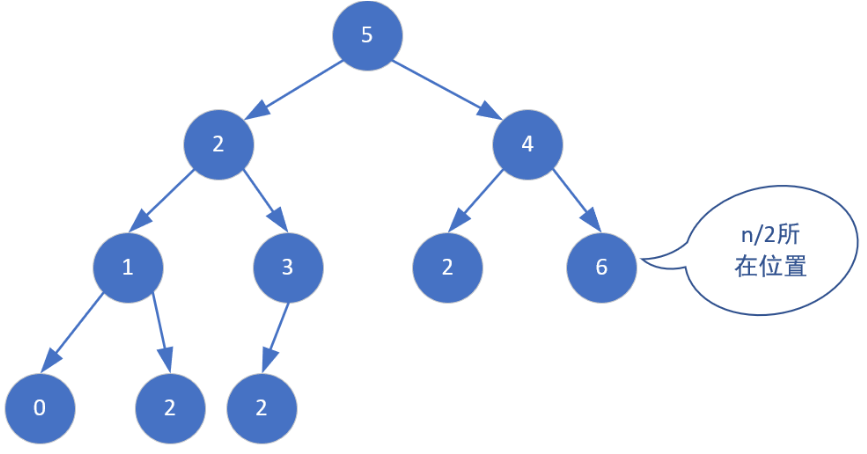
从i=n/2开始每次 i– 并对该位置进行down(i)操作，可以保证每一步都满足down的前提（除了节点x，x的左右子树都满足堆的性质）, 随着i变为1（到达根节点），整个完全二叉树变成了一个小根堆。

1.3 up操作

up(x)是从下往上调整堆，操作如下：若标号为x的父节点比标号为x的节点大（大根堆则反之），则交换它们，然后x移动到它的父节点上。

1
2
3
4
5
6
7
8
void up(int x)
{
    while(x/2 && h[x/2]>h[x])//若x有父节点，且其父节点的值比它大
    {
        swap(h[x/2], h[x]); //将它与父节点交换
        x /= 2;//将x移动到它的父节点上
    }
}

up操作是专门在往堆中加入新元素时使用的。

1.4 插入元素

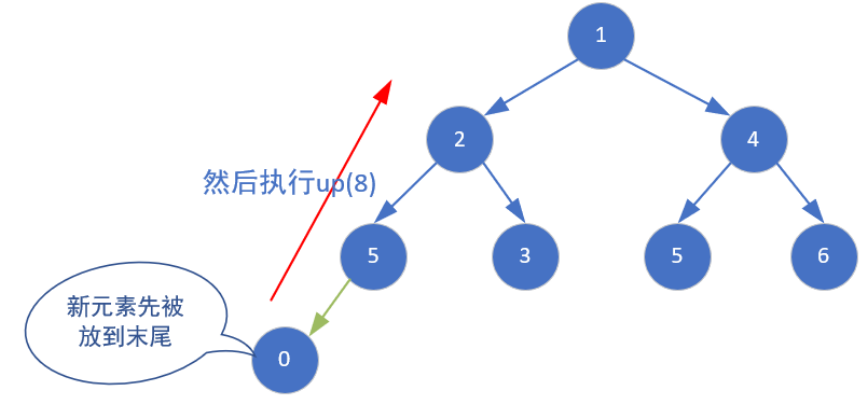
如何往堆中插入一个元素且不破坏堆的结构呢？
把新元素先放到堆数组的末尾，再对它进行up操作即可。

1
2
3
4
5
void push(int value)
{
    h[++size] = value;
    up(size);
}

1.5 弹出堆顶元素

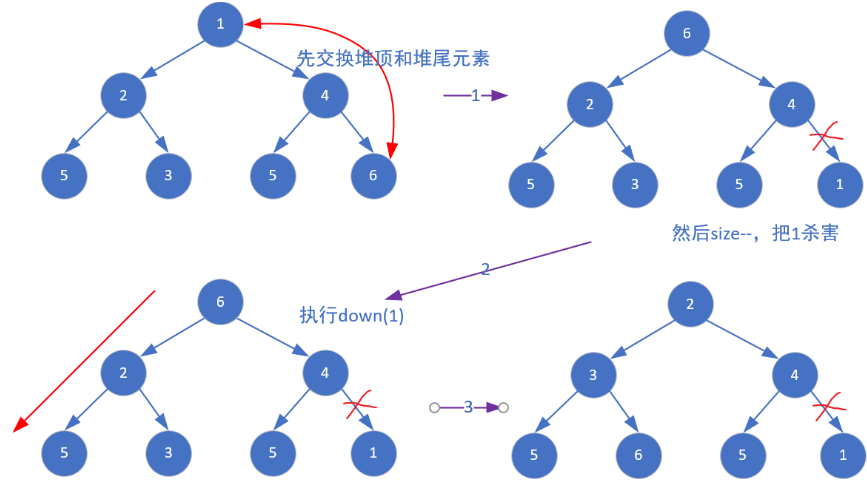
交换堆顶和堆尾元素，然后size–即可，让当前位于堆尾的元素处于假死状态（标记），现在整个结构只有根节点不满足堆的性质了，这时只要对根节点执行down操作即可。

1
2
3
4
5
6
void pop()
{
    swap(h[1], h[size]);
    size--;
    down(1);
}

Dijkstra需要用堆进行优化，碰到有大量取最值操作的问题也要用到堆，其他情况用堆排序就没什么必要了，不如用快排（虽然堆排的最坏情况比快排要好一些，但消耗额外空间）

2. 找出数组中第k大的数

https://leetcode-cn.com/problems/kth-largest-element-in-an-array/

除了快速选择，这题也可以用大根堆做：即将数组中所有元素插入到堆中，然后删除堆顶元素k-1次，此时堆顶元素就是第k大的数。主要用来练习下手写堆。

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
import java.util.ArrayList;
import java.util.List;

class MyHeap{ //实现大根堆
    int[] heap;
    int size;
    MyHeap(int length){
        heap = new int[length*2];
        size = 0;
    }

    public void down(int x){
        int max = x;
        if(x*2<=size && heap[x*2]>heap[max]) max = x*2;
        if(x*2+1<=size && heap[x*2+1]>heap[max]) max = x*2+1;
        if(max==x) return;

        int tmp = heap[max];
        heap[max] = heap[x];
        heap[x] = tmp;

        down(max);
    }

    public void up(int x){
        while(x/2>0 && heap[x]>heap[x/2]){
            int tmp = heap[x];
            heap[x] = heap[x/2];
            heap[x/2] = tmp;

            x/=2;
        }
    }

    public void push(int val){
        heap[++size] = val;
        up(size);
    }


    public void pop(){
        int tmp = heap[size];
        heap[size] = heap[1];
        heap[1] = tmp;

        size--;
        down(1);
    }

    public int peek(){
        return heap[1];
    }
}

class Solution {
    public int findKthLargest(int[] nums, int k) {
        MyHeap h = new MyHeap(nums.length);
        for (int i = 0; i < nums.length; i++) { //将数元素全部插入到堆中
            h.push(nums[i]);
        }
        for (int i = 0; i < k-1; i++) { //pop k-1次，下一次堆顶元素就是第k大的数
            h.pop();
        }
        return h.peek();
    }
}

3. 数据流中的第k大元素

【题目】

https://leetcode-cn.com/problems/kth-largest-element-in-a-stream/

要求设计一个数据结构，每次往该数据结构中add一个元素，都返回add后当前数据结构中倒数第k大的元素。

【解析】

创建一个容量为k+1的小根堆，每次添加后如果超出容量（即元素个数为k+1）了，就删除堆顶元素，然后当前堆顶元素就是当前原数组第k大的元素。

模拟看看，假如初始数组为[4,5,8,2]，然后往其中添加元素的顺序为3,5,10,9,4，k=3 。（假定有序，每一轮添加后的小根堆用中括号标出）

第零次添加：[4] （初始数组）

第一次添加：[4, 5] （初始数组）

第二次添加：[4, 5, 8] （初始数组）

第三次添加：2, [4, 5, 8] （初始数组），添加2后，超出容量，删除堆顶元素（最小值）2，当前堆顶元素4为当前原数组第k大的元素。初始数组阶段，仅仅为了维护当前小根堆的性质，不计入答案。

第四次添加：2, 3, [4, 5, 8]，添加3后，超出容量，删除堆顶元素3，当前堆顶元素4为原数组第k大的元素

第五次添加：2, 3, 4, [5, 5, 8]，添加5后，超出容量，移除堆顶元素4，当前堆顶元素5为原数组第k大元素

第六次添加：2, 3, 4, 5, [5, 8, 10]，同理

第七次添加：2, 3, 4, 5, 5, [8, 9, 10]

第八次添加：2, 3, 4, 4, 5, 5, [8, 9, 10]

上面给出了原数组和容量为k的小根堆之间的关系，可以看出按照该法当前小根堆的堆顶总是当前数据的第k大元素。

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
import java.util.PriorityQueue;

class KHeap{ //最大容量为k的小根堆
    int[] heap;
    int curSize;
    int k;

    KHeap(int k, int[] arr){
        this.k = k;
        this.curSize = 0;
        heap = new int[k+2]; //我们的堆数组从1开始计数，还要留1个空间插入新元素，所有要开k+2
        for (int i = 0; i < arr.length; i++) {
            push(arr[i]);
        }
    }

    public void push(int val){
        heap[++curSize] = val;
        up(curSize);
        while(curSize>k) pop(); //如果当前元素数量大于k，则弹出堆顶元素
    }

    public void pop(){
        int tmp = heap[1];
        heap[1] = heap[curSize];
        heap[curSize] = tmp;

        curSize--;
        down(1);
    }

    public void down(int x){
        int min = x;
        if(x*2 <= curSize && heap[x*2]<heap[min]) min = x*2;
        if(x*2+1 <= curSize && heap[x*2+1]<heap[min]) min = x*2+1;
        if(min==x) return;

        int tmp = heap[min];
        heap[min] = heap[x];
        heap[x] = tmp;

        down(min);
    }

    public void up(int x){
        while(x/2 > 0 && heap[x]<heap[x/2]){
            int tmp = heap[x];
            heap[x] = heap[x/2];
            heap[x/2] = tmp;

            x/=2;
        }
    }

    public int peek(){
        return heap[1];
    }
}

class KthLargest {
    KHeap kh;

    public KthLargest(int k, int[] nums) {
        kh = new KHeap(k, nums);
    }

    public int add(int val) {
        kh.push(val); 
        return kh.peek(); 
    }
}