《哈希表》专题

Posted on In , Views:

关于哈希表的算法。

1. 哈希表

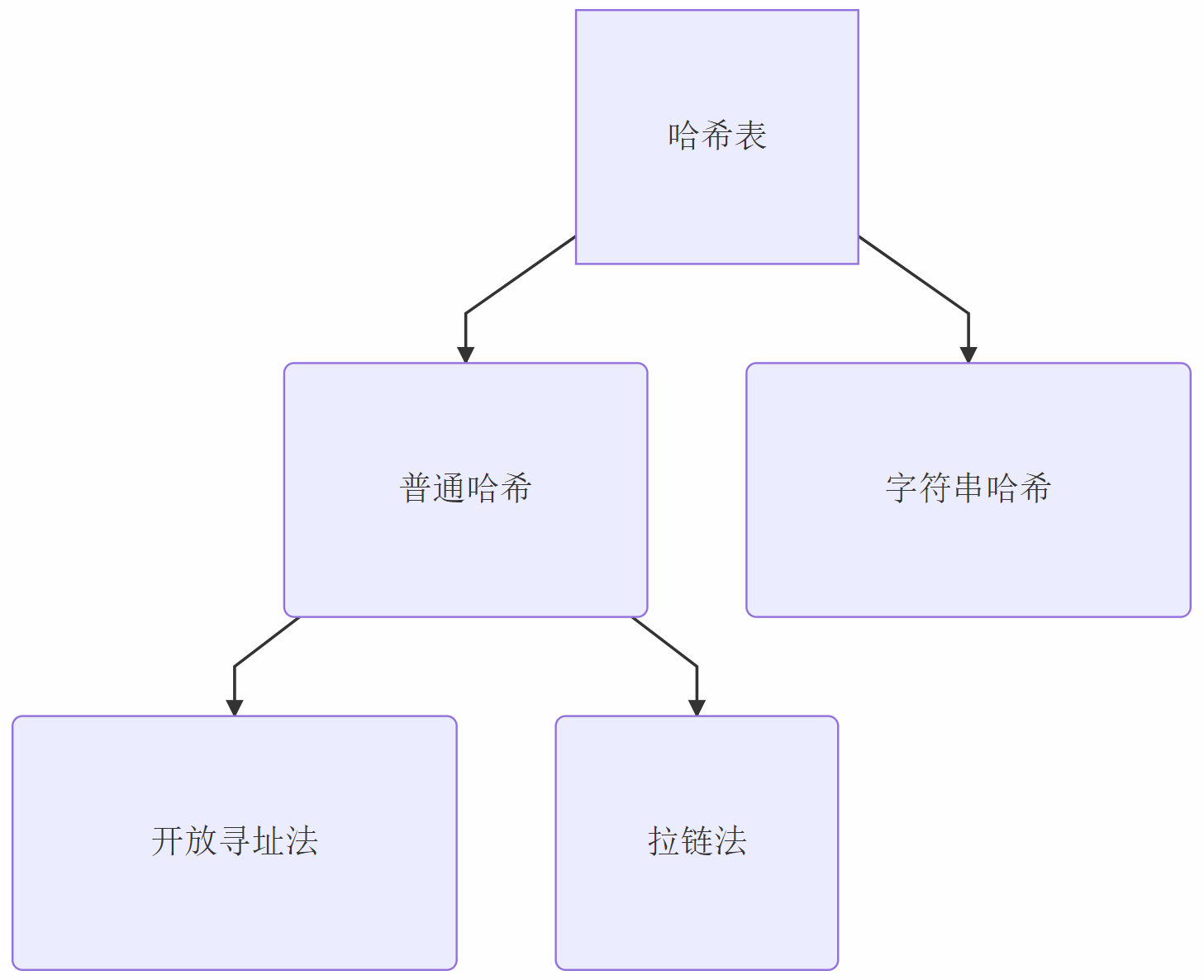
哈希表的主要作用: 查找速度为O(1)。

1.1 普通哈希

如何构造哈希数组？

比如数据的值域为0~99，我们对每一个数据取模，然后把该数据放到哈希数组中取模结果的位置。

哈希数组应该开多大？让每个数对多少取模?

首先明确数据最多会有多少个，假如为N个，则哈希数组的长度就取大于等于N的最小质数P，每个数也都对P取模（P最好离2的整数次幂远些以降低发生冲突的概率）。
比如数据一共会有10个，那我们的N就取11，然后把每个数据放到数组中该数据%11下标位置。

取模后产生位置冲突如何解决？

使用拉链法或者开放寻址法。

1.2 两种哈希表结构

1.2.1 拉链法

其大概结构如下

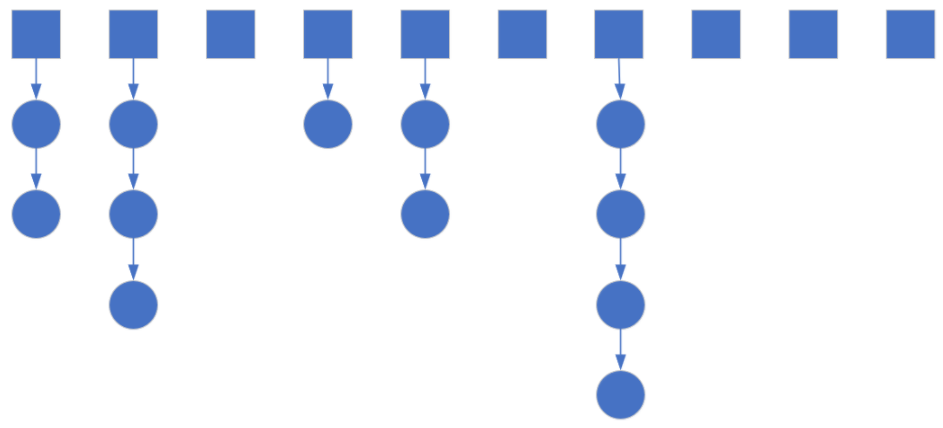
这个数组中的每一个元素其实都是一个链表的头结点（它的值就是链表第一个节点的下标），对每个取模后index相同的数据，就往该链表中插入一个新的节点。（如果有删除的需求，可以在链表的节点中加入一个bool属性，删除它就把它变为FALSE即可）

在学习下面内容之前最好先复习下数组模拟单链表的内容。

向哈希表中新增数据

1
2
3
4
5
6
7
8
9
10
11
12
const int N = 100003;//数据最多有多少个，N就取刚好大于等于的那个质数
int h[N]; //哈希数组，初始化为全-1
int e[N]; //所有节点的值
int ne[N]; //所有节点的next指针
void insert(int value)
{
    int k = (x%N+N)%N; //C++对负数取模会得到负数，+N再%N将其结果变为正数。
    e[idx] = value; //新增一个节点
    /*采用头插法添加新节点*/
    ne[idx] = h[k]; //让新节点的next指向该链表的第一个节点。注意h[k]是哈希数组下标k位置所对应链表的头结点，它的值就是这个链表第一个节点的下标
    h[k] = idx++; //让头结点指向新节点
}

查询某数据是否在哈希表中

1
2
3
4
5
6
7
8
9
10
11
12
bool find(int value)
{
    int k = (x%N+N)%N; //寻找哈希值
    int temp = h[k]; //获取哈希值位置链表的头结点
    while(true) 
    {
        if(temp==-1) break; //链表遍历完毕，跳出循环
        if(e[temp]==value) return true;//如果某节点的值等于value，说明哈希表中存在此元素
        temp = ne[temp];//遍历指针走向链表的下一个节点
    }
    return false;//哈希表中找不到value
}

1.2.2 开放寻址法

把哈希数组开到数据总个数的2~3倍。如果插入数据的位置发生冲突，则会不断向右寻找下一个空位插入。
开放寻址法只需要一个find(value)函数，它的作用是先按上述规则寻找value，如果找到了则返回value所在的下标，如果没找到就在下一个可用空位插入value，并返回这个空位的下标。

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
const int N = 200003;//假如数据总个数为100000，我们的N取大于等于它两倍的最小质数
const int null = 0x3f3f3f3f;//用无穷大模拟null，表示哈希数组的某个位置未被占用
int h[N];//全部初始化为0x3f
int find(int value)
{
    int k = (value%N+N)%N; //计算哈希值k
    while(h[k] != null && h[k] != value)//当k位置被占用，且占用的值不等于vaue
    {
            k++;//继续向右寻找
            if(k==N) k = 0; //在整个数组中不断的寻找，直到找到为止。因为数组长度为数据总个数的两倍，这个空位总能够找到。
    }
    return k;//若找到了value，就返回value的下标；若没找到，就返回一个合理的空位下标，value应该被存在这个位置中。
}

/*向哈希表中添加某value*/
h[find(value)] = value;
/*查询哈希表中是否存在某value*/
if(h[find(v)]!=null) printf("Yes\n");
else printf("No\n");

1.2.3 取0x3f3f3f3f为无穷大的好处

  1. 首先它换算成10进制刚好超过$10^9$，而一般算法的数据规模都不会超过$10^9$。
  2. 其次它即使乘以2也不会溢出，满足了无穷大+无穷大=无穷大的定义。
  3. 再者如果想把某个数组的全部元素初始化为无穷大，因为memset是以字节为单位的，所以memset(arr, 0x7fffffff, sizeof arr)是行不通的（7fffffff都4个字节了）。想把数组内容全部初始化真正的最大值0x7fffffff，只能写循环赋值。而如果把最大值定为0x3f3f3f3f，因为形式上是3f的循环，3f刚好占一个字节，所以直接memset(arr, 0x3f, sizeof arr)即可。（这也是为什么memset一般都用来初始化为0（16进制为4个00字节）或-1（16进制为4个FF字节）

1.3 字符串哈希

简单来说，就是把每个字符串按照某种算法解释为一个数字，这个数字就是该字符串的哈希值。

将字符串的所有前缀进行哈希处理

如果已知某个字符串所有前缀的哈希值hash[i]，就可以在O(1)的时间内求出它子串(下标l与r之间)的哈希值: $result = hash[r]-hash[l-1]* p^{r-l+1}$

求字符串某一前缀哈希值的栗子

假定字符串的某前缀为hello，把它看作是一个P进制的数，将它转化为10进制。（假定进制P=131, 字母a~z映射到它们自己的ASCII码值）

要注意不能把任意单个字母映射为0，否则假如把A映射为0，则A, AA, AAA…都相等了

$$
104*(131^4)+101*(131^3)+108*(131^2)+108*(131^1)+111*(131^0)=30855091530
$$

然后将这个十进制的结果对Q取余（这里Q我们取为$2^{64}$，也就是unsigned long long的自然溢出）
结果为30855091530，把它保存在哈希数组下标5的位置（字符串下标从1开始，hash[5]表示字符串下标1~5子串的哈希值）。要注意的是，这个哈希数组的数据类型应该为unsigned long long（下面简称ULL），因为我们是利用它的自然溢出来哈希的。

模板

根据经验，P取为131或13331，Q取为$2^{64}$，在这样的情况下99.99%不会发生冲突。

Q取为$2^{64}$（ULL类型数据的最大值+1），也就是直接把ULL类型数据的自然溢出视为哈希运算，所以我们直接把哈希数组初始化为ULL类型。为了提高查询效率，我们可以预处理字符串每一位的权值，保存在数组w中（也是ULL类型）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
typedef unsigned long long ULL;
ULL h[N],w[N];//hash数组和权值数组
const int P = 131;
w[0] = 1;//第一个前缀子串只有一个字符，它的权值为1
/*获取字符串的所有前缀哈希，初始化权值数组*/
for(int i = 1; i<=n; i++)
{
    h[i] = h[i-1]*P+s[i];//s是一个用字符串表示的P进制数，这句的意思是把数组s的所有前缀都视为一个P进制数，然后把它们全部转换为十进制数存入h数组（也就是字符串前缀哈希的过程）
    w[i] = w[i-1]*P;//预处理P进制数每一项的权值
}
/*拿到字符串的前缀hash数组和预处理好的weigh数组后，我们就可以根据公式计算该字符串任意子串的哈希值了*/
ULL get(int l, int r)
{
    return h[r]-h[l-1]*w[r-l+1];
}

2. two sum

【题目】

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。

假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

示例:

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]

【解析】：

暴力解法（平方时间复杂度）不说了，主要讨论利用哈希表求解（线性时间复杂度）的方法。

思路：遍历数组中的所有元素，每次遍历都检查hashtable中有没有target-nums[i]，如果存在，则哈希表中记录的target-nums[i]的下标与i就是答案，否则将（nums[i]，i）存到hashmap中，继续下一轮循环。

这种方法每次搜索元素不用遍历数组，而是在哈希表中寻找，因为哈希表的查询速度极快（常数级），因此时间复杂度降低到线性。

【ac代码】：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> hashTable;
        vector<int> re;
        int length = nums.size();
        for(int i = 0;i<length;i++)
        {
            auto another = hashTable.find(target-nums[i]); //在哈希表中寻找能与nums[i]相加等target的目标元素
            if(another != hashTable.end())  // 如果找到了，返回答案
            {
                re.push_back(another->second);
                re.push_back(i);
                break;
            }
            hashTable[nums[i]] = i; //如果没找到，把当前元素nums[i]及其下标i加入哈希表，开始下一轮循环
        }
        return re;
    }
};

3. 大餐计数

【题目】

https://leetcode-cn.com/problems/count-good-meals/

大餐 是指 恰好包含两道不同餐品 的一餐，其美味程度之和等于 2 的幂。

你可以搭配 任意 两道餐品做一顿大餐。

给你一个整数数组 deliciousness ，其中 deliciousness[i] 是第 i 道餐品的美味程度，返回你可以用数组中的餐品做出的不同 大餐 的数量。结果需要对 109 + 7 取余。

注意，只要餐品下标不同，就可以认为是不同的餐品，即便它们的美味程度相同。

示例 1：

1
2
3
4
输入：deliciousness = [1,3,5,7,9]
输出：4
解释：大餐的美味程度组合为 (1,3) 、(1,7) 、(3,5) 和 (7,9) 。
它们各自的美味程度之和分别为 4 、8 、8 和 16 ，都是 2 的幂。

示例 2：

1
2
3
输入：deliciousness = [1,1,1,3,3,3,7]
输出：15
解释：大餐的美味程度组合为 3 种 (1,1) ，9 种 (1,3) ，和 3 种 (1,7) 。

提示：

  • 1 <= deliciousness.length <= 10^5
  • 0 <= deliciousness[i] <= 2^20

【解析】

本题简单来说就是寻找在数组中有多少个数对，这些数对的和是2的幂。

注意题目给出数组中每一个元素的最大值为2^20，那么两个元素的和最大值为2^21，在[0 ~ 2^21]这个范围内2的幂并不多，因此在遍历数组时，对每一个元素x，遍历[0 ~ 2^21]这个范围内所有2的幂m，在哈希表中查找是否存在m-x，如果存在说明找到了一个和为2的幂的数对。

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int countPairs(vector<int>& deli) {
        int re = 0;
        unordered_map<int, int> hash;

        int length = deli.size();
        for(int i = 0;i<length;i++){
            int val = deli[i];
            
            //遍历[0 ~ 2^21]这个范围内所有2的幂m
            for(int j = 0;j<=21;j++){ 
                if(hash.count((1<<j)-val)){ //如果哈希表中存在(m-val)，则把数组中下标i之前所有值为(m-val)的元素出现次数加到答案中
                    re = (re + hash[(1<<j)-val]) % (1e9+7);
                }
            }
            hash[val]++; //将val记录到哈希表中
        }
        return re;
    }
};