《队列》专题
队列相关的数据结构和算法。
1. 单调队列
应用:求滑动窗口中的最值。
比如4,5,2,1,-1,3,5
假设窗口大小为3,每次移动一位,输出每次移动后区间中的最小值。
如果用暴力做法,每次移动都要遍历整个窗口寻找,时间复杂度为:移动次数X3
在暴力做法的基础上,我们发现滑动窗口每移动一次,如果新加入的数比它左边的数小,则左边的数在之后的判定中就一定不会是最小值,可以跳过对它的判断来降低时间复杂度。
用双端队列来模拟这个过程,每次新加入的元素n与窗口中其他元素(如a, b, c)逐一比较,比如n比c小,就把c给pop掉,直到n的左侧没有元素比它更大了,就将n给push到队列尾部。
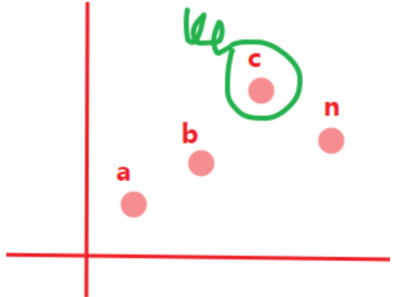
这样就保证我们的窗口队列在每次迭代完后都是单调的,每次移动窗口的最小值就是队列头的值。
我们可以用双端单调队列来完成这件事。要注意的是,因为涉及到删除元素,队列维护的元素必须是原数组的下标,否则难以判断窗口大小是否越界(如此例中>3)。
模拟样例
| 原数组a | 双端队列q | 解释 |
|---|---|---|
| [(4), 5, 1, 1, 3] | [0] | 单调队列要先填入一个初始0,因为原数组的第一个元素一开始必然是最小值。min=a[q[0]]=4 |
| [(4, 5), 1, 1, 3] | [0, 1] | 5比4大,4下次还可能是最小值。所以不需pop掉4,而是直接让5进队。min=a[q[0]]=4 |
| [(4, 5, 1), 1, 3] | [2] | 1小于4和5,只要1在窗口中,答案永远都不可能是4或5,所以队列中4和5的下标都被pop,只剩1的下标2。min=a[q[0]]=1 |
| [4, (5, 1, 1), 3] | [3] | 又进来一个1,相等时我们把原有的重复元素全部pop,队头元素被更新为3。min=a[q[0]]=1 |
| [4, 5, (1, 1, 3)] | [3, 4] | 3比1大,把3加入队列。min=a[q[0]]=1 |
每次操作要检查窗口大小,如果大了就要把队头pop掉。检查的方法很简单:
1 | if(q[q.size()-1]-q[0]+1>=k) pop q.front(); |
模板
1 | q.push_back(0); |
因为要使用pop_back()所以我们得用双端队列deque。
1.1 滑动窗口的最大值
【题目】
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/sliding-window-maximum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
【ac代码】
1 | class Solution { |
求最小值同理,自己尝试写出。