《链表》专题

Posted on 2020-11-21 Edited on 2021-01-23 In 计算机 , 数据结构与算法 Views:

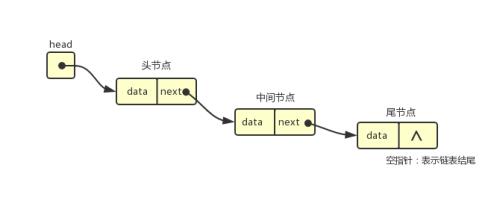
0. 数组模拟链表

本质上就是实现了一个memory allocator，追求运行效率放弃可读性和拓展性，一般不会在工程中使用。

假如要往链表中存入非常多的数据，如果使用指针实现的链表（创建node类，每存入一个数就要new一个node），它的速度相对较慢。而数组模拟的链表可以完成指针链表所能完成的所有操作，且创建新节点就是给数组某个位置赋值，所以速度比指针链表快的多。并且数组还可以被模拟用于存储树和图，因此掌握数组模拟数据结构是十分必要的。

思路

定义模拟要用到的变量：

e[ ] 数组相当于用来存储链表节点的内存空间，i代表节点i的地址，e[i]代表节点i的值
ne[i] 表示节点i的next指针（空节点的下标为-1，如果数组中下标为3的节点就是尾节点了，则ne[3]=-1），里面的值就是节点i的next指针指向的元素在内存数组e中的位置
head 表示第一个节点的下标
idx 表示e数组当前可用的位置，即下一块可分配内存的地址

栗子

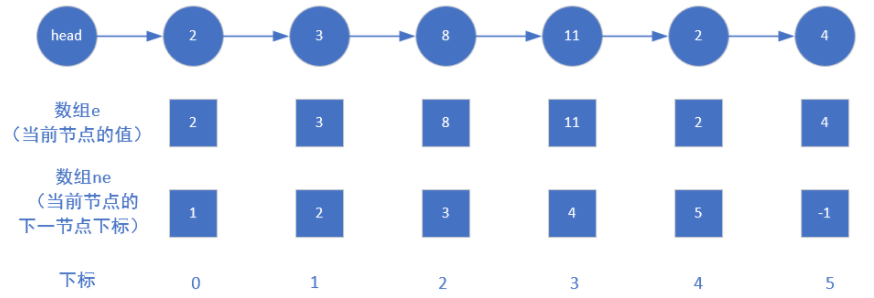
假如要模拟如下链表

模拟完成后数组e和ne的状态如下

模板如下

0.1 初始化

int N = 100010; //链表最大节点数
int head, e[N], ne[N], idx;
void init()
{
    for(int i = 0;i<N;i++) ne[i] = -1; //ne[N]初始化为-1
    head = -1; //一开始没有节点，因此第一个节点的位置为-1
    idx = 0; //数组中没有任何数据，所以下一个可用的位置为0
}

0.2 插入新节点

0.2.1 新节点插入链表的头部

void AddToHead(int value)
{
    e[idx] = value; //把新节点放在内存数组当前可用位置
    ne[idx] = head;//让新节点的next指针指向第一个节点（head表示第一个节点的下标）
    head = idx;//让head指向新节点，使它变为第一个节点
    idx++;//数组当前的可用位置往右走一格
}

0.2.2 新节点插入下标为k的节点之后

void Add(int value, int k)
{
    /*为了健壮性可以判断k的上一个位置的next是否等于-1*/
    e[idx] = value; //把新节点放在数组当前可用位置
    ne[idx] = ne[k]; //让新节点的next指向k节点的next
    ne[k] = idx;//让k节点的next指向新节点
    idx++;//数组当前的可用位置往右走一格
}

0.3 删除下标为k的后面一个节点

void Delete(int k)
{
    ne[k] = ne[ne[k]];
}

1. 环形链表

1.1 环形链表Ⅰ

【题目】

Given head, the head of a linked list, determine if the linked list has a cycle in it.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to.

**Note that pos is not passed as a parameter **.

Return true if there is a cycle in the linked list. Otherwise, return false.

Follow up:

Can you solve it using O(1) (i.e. constant) memory?

《哈希表法》

【解析】

很容易想到的一种解法就是遍历链表的每一个节点，每经过一个节点就把该节点记录到哈希表中，随后每经过一个节点就去哈希表中查找这个节点是否存在，如果存在就是有环。

这种方法需要消耗比较多的空间，其实这类题可以用一种更巧妙的方法求解。

【ac代码】

class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode* cur = head;
        unordered_map<ListNode*, int> hashmap;
        
        while(cur!=NULL) //遍历链表
        {
            auto value = hashmap.find(cur);  //在哈希表中查找当前节点是否已经被遍历过
            if(value!=hashmap.end()) return true; //如果在哈希表中能查到，说明链表存在环
            hashmap[cur] = 1; //在哈希表中找不到，就把这个节点的信息存入哈希表
            cur = cur->next;
        }
        return false;
    }
};

《快慢指针法》

【解析】

使用快慢指针（比如慢指针每次前进一步，快指针每次前进两步）。如果链表中存在环，那么快慢指针迟早会相遇。

这种方法比哈希表解法快的多，也节省了大量的空间。

【ac代码】

class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(head==NULL || head->next==NULL) return false;
        ListNode* fast = head->next;
        ListNode* slow = head;
        while(fast!=slow)
        {
            //如果快指针走到链表尽头，说明链表没有环
            if(fast==NULL || fast->next==NULL) return false;
            
            fast = fast->next->next;
            slow = slow->next;
        }
        return true;       
    }
};

1.2 环形链表Ⅱ

【题目】

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to. Note that pos is not passed as a parameter.

Notice that you should not modify the linked list.

Follow up:

Can you solve it using O(1) (i.e. constant) memory?

《哈希表法》

【解析】

做过环形链表Ⅰ，第一个想到的办法就是哈希表了。只需要在环形链表Ⅰ的解法中，当在哈希表中找到已存在的节点时，把这个节点返回即可。

【ac代码】

时间复杂度与空间复杂度都为O(n)

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        unordered_map<ListNode*, int> hashmap;
        ListNode* cur = head;
        while(cur!=NULL)
        {
            auto another = hashmap.find(cur); //在哈希表中寻找是否存在当前节点cur
            if(another!=hashmap.end()) return cur; //如果找到了，直接返回节点cur
            hashmap[cur] = 1;	//没找到的话，就把cur存入哈希表
            cur = cur->next;
        }
        return NULL;
    }
};

《双指针法》

【解析】

双指针解法需要一些数学证明，这里直接上结论，快慢指针（快一次走两步，慢一次一步）同时从head出发，如果链表存在环，那么第一次快慢指针相遇时将快指针重新放到head并将其放慢（与慢指针同速），第二次快慢指针相遇的节点就是环的入口。

【ac代码】

时间复杂度线性，空间复杂度常数

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(head==NULL || head->next==NULL) return NULL;
        ListNode* fast = head;
        ListNode* slow = head;
        
        /*让快慢指针第一次相遇*/
        do
        {
            if(fast==NULL || fast->next==NULL) return NULL;
            fast = fast->next->next;
            slow = slow->next;          
        } while(fast!=slow);
        
        fast = head; //将快指针移动到head
        
        /*将快指针放慢，它和慢指针再次相遇的节点就是环的入口*/
        while(fast!=slow)
        {
            fast = fast->next;
            slow = slow->next;          
        } 
        
        return fast;
    }
};

2. 链表中点

《快慢指针法》

【题目】给定链表，返回链表中点（如果有两个则返回后者）

【解析】

快慢指针。慢指针一次一步，快指针一次两步，当快指针走到头时，慢指针就是链表中点。

【ac代码】

快慢指针

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        if(head==NULL) return NULL;
        ListNode* slow = head; 
        ListNode* fast = head;
        
        while(fast)
        {
            if(!fast->next) break;
            slow = slow->next;
            fast = fast->next->next;
        }
        
        return slow;
    }
};

《数组法》

【解析】

把链表所有节点放到数组中，取下标n/2的节点

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
private:
    vector<ListNode*> vec;
public:
    ListNode* middleNode(ListNode* head) {
        if(head==NULL) return NULL;
        ListNode* cur = head;
        
        /*把链表所有节点放入数组*/
        while(cur)
        {
            vec.push_back(cur);
            cur = cur->next;
        }
        
        int length = vec.size();
        return vec[length/2]; //取数组中点元素即可
    }
};

《单指针法》

【解析】

先遍历一遍链表得知长度，然后重新遍历到n/2个节点即可

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        if(head==NULL) return NULL;
        ListNode* cur = head;
        
        /*计算链表总长*/
        int length = 0;
        while(cur)
        {
            cur = cur->next;
            length++;
        }
        
        /*走到总长的1/2处获取中点*/
        cur = head;
        for(int i = 0;i<length/2;i++)
        {
            cur = cur->next;
        }
        return cur;
    }
};

3. 旋转链表

【题目】

给定一个链表，旋转链表，将链表每个节点向右移动 k 个位置，其中 k 是非负数。

示例 1:

输入: 1->2->3->4->5->NULL, k = 2
输出: 4->5->1->2->3->NULL
解释:
向右旋转 1 步: 5->1->2->3->4->NULL
向右旋转 2 步: 4->5->1->2->3->NULL

示例 2:

输入: 0->1->2->NULL, k = 4
输出: 2->0->1->NULL
解释:
向右旋转 1 步: 2->0->1->NULL
向右旋转 2 步: 1->2->0->NULL
向右旋转 3 步: 0->1->2->NULL
向右旋转 4 步: 2->0->1->NULL

【解析】

首先获取链表长度，然后计算移动k个位置后新链表的头尾节点位置，最后将头尾重新连接即可。

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* rotateRight(ListNode* head, int k) {
        /*计算链表的长度*/
        int length = 0;
        ListNode* cur = head;
        while(cur)
        {
            length++;
            cur = cur->next;
        }  
        
        /*特殊情况*/
        if(length==1 ||length==0 || k%length==0) return head;
        
        /*从头节点开始向右移动k步后所在位置节点就是新链表尾，其下一个节点就是新链表头*/
        k = length - k % length - 1; 
        cur = head;
        while(k--) cur = cur->next;
        ListNode* newTail = cur;
        ListNode* newHead = cur->next;
        
        
        /*按照新链表头尾重新拼接链表*/
        while(cur->next) cur = cur->next; //先将cur移动到原链表的尾部
        cur->next = head;				//尾巴接到头上
        newTail->next = NULL;			//新尾巴的next节点置NULL
        return newHead;					
    }
};

4. 反转链表

【题目】反转链表

【解析】用两个辅助指针（prev、tail），和一个工作指针（cur），辅助指针在cur的一前一后，prev用来给next指，tail保证链不断

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* prev = NULL;
        ListNode* cur = head;
        ListNode* tail = head;
        while(cur)
        {
            tail = tail->next; //tail先前进一步，存储下一个节点
            cur->next = prev;  //反转操作
            prev = cur;		  //prev指针走到cur的位置
            cur = tail;		  //cur走到tail的位置
        }
        return prev;
    }
};

5. 排序链表

【题目】

要求时间复杂度O(nlogn)，且空间复杂度为常数级。因此不能使用上次写过的插入排序。

【解析】

参考了官方题解。

需要两个子方法：

合并两个链表使其有序
寻找链表中点

就可以组合成归并排序了。

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    /*有序地合并两个有序链表*/
    ListNode* mergeTwoLists(ListNode* head1, ListNode* head2)
    {
        ListNode* dumpHead = new ListNode();
        ListNode* opa = dumpHead;
         
        ListNode* cur1 = head1;
        ListNode* cur2 = head2;
        while(cur1 && cur2)
        {
            if(cur1->val < cur2->val)
            {
                opa->next = cur1;
                cur1 = cur1->next;
            }
            else 
            {
                opa->next = cur2;
                cur2 = cur2->next;
            }
            opa = opa->next;
        }
        if(cur1) opa->next = cur1;
        if(cur2) opa->next = cur2;
        return dumpHead->next;
    }

    ListNode* sorting(ListNode* head, ListNode* tail)
    {
        if(!head) return NULL; //当head为NULL时的特判
        if(head->next==tail)   //当前递归的子链表中如果只包含一个节点的特判
        {
            head->next = NULL;
            return head;
        }
        /*寻找当前子链表的中点*/
        ListNode* fast = head, *slow = head;
        while(fast!=tail)
        {
            fast = fast->next;
            slow = slow->next;
            if(fast!=tail) fast = fast->next;
        }
        ListNode* mid = slow;
        
        //归并
        return mergeTwoLists(sorting(head, mid), sorting(mid, tail));
    }

    ListNode* sortList(ListNode* head) {
        return sorting(head, NULL);
    }
};

6. 重排链表

【题目】

Given a singly linked list L: L0→L1→…→Ln-1→Ln,
reorder it to: L0→Ln→L1→Ln-1→L2→Ln-2→…

You may not modify the values in the list’s nodes, only nodes itself may be changed.

【解析】

将链表节点装进数组，然后对数组进行操作即可。

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
private:
    vector<ListNode*> arr;
public:
    void reorderList(ListNode* head) {
        if(head==NULL) return;
        ListNode* cur = head;
        
        /*将链表装进数组*/
        while(cur)
        {
            arr.push_back(cur);
            cur = cur->next;
        }

        
        int length = arr.size();
        int i = 0, j = length-1;
        /*按题目要求将所有节点next重新连接*/
        while(1)
        {
            arr[i]->next = arr[j];
            if(i==j) break; // 必须在i++和j--之前判断i是否等于j，手动模拟一遍即可理解
            i++;
            
            arr[j]->next = arr[i];
            if(i==j) break;
            j--;
        }

        arr[i]->next = NULL; //最后一个访问到的节点成为新链表的尾节点
        return;

    }
};

7. 对链表进行插入排序

【题目】

对链表进行插入排序。首先要知道对数组进行插入排序的原理是啥。

{连接到排序算法笔记}

【解析】

假定有哑节点。

先从大的方向考虑，可以使用两个指针，一个指针cur指向当前【待插入有序部分的元素】，一个指针opa指向哑节点，每次从[opa, cur) 这个区间（即链表中当前的有序部分）中找出这样一个节点FOO，它的下一个节点的值严格大于cur节点的值，然后把cur节点插入到这个节点之后。

因为每次执行插入操作时，cur节点的位置需要移动，为了不丢失cur->next这个节点，我们设置一个save节点，它总是指向cur的上一个节点。

每次找出节点FOO后，可能出现两种情况：

FOO的下一个就是cur节点。这种情况下cur所在节点不需要移动，我们只需让cur继续往下走即可
FOO的下一个不是cur节点。这种情况下，首先利用save指针保存cur的下一个节点，然后将cur插入到FOO的后面，然后把cur移动到save的位置。这就等同于数组插入排序中的插入这一步。

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* insertionSortList(ListNode* head) {
        ListNode* cur = head; //总是指向待插入有序部分的节点
		
        /*哑节点*/
        ListNode* dummyHead = new ListNode();
        dummyHead->next = head;

        ListNode* save = dummyHead; //用来保证链表不断，save总是指向cur指针的前一个位置
        ListNode* opa = new ListNode(); //用来在有序部分寻找FOO节点的指针
        while(cur)
        {
            opa = dummyHead; //每次循环开始将opa初始化到哑节点位置
            
            //在当前链表的有序部分中寻找节点FOO的循环，FOO的下一个节点的值严格大于cur节点的值
            while(opa->next!=cur && (opa->next->val <= cur->val)) opa = opa->next;
            //现在opa指向FOO节点了
            
            /*第一种情况*/
            if(opa->next == cur)
            {
                cur = cur->next;
                save = save->next;
                continue;
            }  
			
            /*第二种情况*/
            save->next = cur->next;
            cur->next = opa->next;
            opa->next = cur;
            cur = save->next;
        }
        return dummyHead->next;
    }
};

总结来看，首先从大的方向上确定解题的大体思路，然后分情况讨论，最后处理边界问题。

8. 合并两个有序链表

【题目】

示例：

1 2	输入：1->2->4, 1->3->4 输出：1->1->2->3->4->4

【解析】

两个指针分别指向两个链表，不断移动，将较小的那个连接到答案链表上。

ps：哑节点经常可以统一解决不同corner case（尤其是链表问题），让代码更加简洁。

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* head1, ListNode* head2)     {
        ListNode* dumpHead = new ListNode(); //创建哑节点
        ListNode* opa = dumpHead;			//操作指针
         
        /*分别在两个链表上移动的操作指针*/
        ListNode* cur1 = head1;
        ListNode* cur2 = head2;
        
        /*归并操作*/
        while(cur1 && cur2)	
        {
            if(cur1->val < cur2->val)
            {
                opa->next = cur1;
                cur1 = cur1->next;
            }
            else 
            {
                opa->next = cur2;
                cur2 = cur2->next;
            }
            opa = opa->next;
        }
        if(cur1) opa->next = cur1;
        if(cur2) opa->next = cur2;
        return dumpHead->next;
    }
};

9. 删除中间结点

【题目】

只给链表中的一个节点，从逻辑上删除它

【解析】

将下一个节点的值赋予当前节点，然后让当前节点的next指向下下个节点

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    void deleteNode(ListNode* node) {
        node->val = node->next->val;
        node->next = node->next->next;
    }
};

10. 两数相加

10.1 两数相加Ⅰ

【题目】

You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.

You may assume the two numbers do not contain any leading zero, except the number 0 itself.

Example 1:

l1: 2→4→3

l2: 5→6→4

结果: 7→0→8

Input: l1 = [2,4,3], l2 = [5,6,4]
Output: [7,0,8]
Explanation: 342 + 465 = 807.

Example 2:

Input: l1 = [0], l2 = [0]
Output: [0]

Example 3:

Input: l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
Output: [8,9,9,9,0,0,0,1]

【解析】

这题是用链表实现大数相加。

逆序存储刚好方便做加法（因为本来加法就是从低位到高位），就跟用数组模拟的加法一样操作：用一个t作为进位标志，两链表双指针，用t存储对应数位上相加的结果，将t%10接到答案链表的尾部，然后令t/=10（若t大于10，则变1，相当于进一位；若小于10，则变0，相当于没进位），让t参与下一次迭代运算。

要注意的是，迭代完毕退出循环后，要判断t是否为1，也就是最后一次运算是否产生了进位，若为1则要将其追加在答案尾部。

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    /*创建数据字段为val的新节点，将其追加到以dumpyHead为哑头节点的链表尾部*/
    void AddToTail(ListNode* dumpyHead, int val)
    {
        ListNode* newNode = new ListNode(val);
        ListNode* cur = dumpyHead;
        while(cur->next)
        {
            cur = cur->next;
        }
        cur->next = newNode;
    }

    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode* cur1 = l1, *cur2 = l2;
        ListNode* dumpyHead = new ListNode();
        
        int t = 0; //进位标志
        while(cur1 || cur2)
        {
            if(cur1)
            {
                t+=cur1->val;
                cur1 = cur1->next;
            }
            if(cur2)
            {
                t+=cur2->val;
                cur2 = cur2->next;
            }
            AddToTail(dumpyHead, t%10);//将两位数字相加的结果的个位追加到答案链表尾部
            t/=10; //若t大于10，则变1，相当于进一位；若小于10，则变0，相当于没进位
        }
        if(t) AddToTail(dumpyHead, 1); //最后一次运算是否产生进位

        return dumpyHead->next;
    }
};

10.2 两数相加Ⅱ

【题目】

给你两个非空链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。

你可以假设除了数字 0 之外，这两个数字都不会以零开头。

进阶：

如果输入链表不能修改该如何处理？换句话说，你不能对列表中的节点进行翻转。

示例：

输入：(7 -> 2 -> 4 -> 3) + (5 -> 6 -> 4)
输出：7 -> 8 -> 0 -> 7

【解析】

先用数组存放两个链表的值，然后用数组实现大数相加，再把结果腾到新链表中。

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    /*数组实现大数相加，数组中小下标对应数字高位*/
    vector<int> add(vector<int> v1, vector<int> v2) 
    {
        vector<int> re;
        int length1 = v1.size();
        int length2 = v2.size();
        int i = length1-1, j = length2-1;
        int t = 0;
        while(i>=0 || j>=0)
        {
            if(i>=0) t+=v1[i--];
            if(j>=0) t+=v2[j--];
            re.push_back(t%10);
            t/=10;
        }
        if(t) re.push_back(1);
        return re;
    }
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        vector<int> v1, v2;
        ListNode* cur1 = l1, *cur2 = l2;
        /*将链表中的值挪到数组中*/
        while(cur1)
        {
            v1.push_back(cur1->val);
            cur1 = cur1->next;
        }
        while(cur2)
        {
            v2.push_back(cur2->val);
            cur2 = cur2->next;
        }
        
        vector<int> foo = add(v1, v2); //获取结果数组
        
        /*将结果数组转为结果链表*/
        ListNode* re = new ListNode(foo[foo.size()-1]);
        ListNode* newHead = re;
        for(int i = foo.size()-2; i>=0; i--)
        {
            ListNode* newNode = new ListNode(foo[i]);
            re->next = newNode;
            re = re->next;
        }
        return newHead;

    }
};

11. 删除排序链表中的重复元素

【题目】

给定一个排序链表，删除所有重复的元素，使得每个元素只出现一次。

示例 1:

输入: 1->1->2
输出: 1->2

示例 2:

输入: 1->1->2->3->3
输出: 1->2->3

【解析】

遍历的过程中判断，有重复就删除节点即可

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        ListNode* cur = head;
        while(cur)
        {
            //如果cur没有走到链表尾，且当前节点元素等于下一节点元素
            while(cur->next && cur->val == cur->next->val)
            {
                cur->next = cur->next->next; //删除下一节点
            }
            cur = cur->next;
        }
        return head;
    }
};

12. 删除排序链表中的重复元素Ⅱ

【题目】

给定一个排序链表，删除所有含有重复数字的节点，只保留原始链表中没有重复出现的数字。

示例 1:

输入: 1->2->3->3->4->4->5
输出: 1->2->5

示例 2:

输入: 1->1->1->2->3
输出: 2->3

【解析】

在排序链表中找到存在重复的元素很简单，跟12题一样，只需要判断它与它的下一个节点值是否相等就行，不过这题要把重复元素删干净，也就是说，可能要删除当前已经走到的节点，立刻想到使用prev指针，它总是指向cur的上一个节点。

prev指针的移动分为两种情况：一种是cur没有碰到重复元素，那么prev直接往下移动即可；另外一种是cur碰到重复元素，这时prev要将所有的重复元素删除（改变prev-next的指向）。必须确保prev总是cur的上一个节点。

有了这个思路，剩下的代码细节只需要手动模拟一遍即可。

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        /*链表问题设置一个哑节点方便处理*/
        ListNode* dumpyHead = new ListNode(0);
        dumpyHead->next = head;

        ListNode* prev = dumpyHead; //总是指向cur的上一个节点
        ListNode* cur = head;
        while(cur)
        {
            int flag = 0; //cur是否碰到重复元素 
            
            /*如果cur没有走到链表尾，且当前节点值等于下一节点值*/
            while(cur->next && cur->val == cur->next->val)
            {
                cur->next = cur->next->next; //删除下一节点
                flag = 1; //进入该循环代cur碰到了重复元素
            }
            if(flag) prev->next = prev->next->next; //如果cur碰到重复元素， 则利用prev指针删除所有重复元素，另外这句话也保证了prev总是cur的上一个节点
            else prev = prev->next; //否则正常移动即可

            cur = cur->next;
        }
        
        return dumpyHead->next; //head可能是一个重复元素，因此必须返回哑节点的next指针
    }
};

13. 设计链表

class Node
{
public:
    int val;
    Node* next;
    Node(int value)
    {
        this->val = value;
        this->next = NULL;
    }
    Node()
    {

    }
};

class MyLinkedList {
public: 
    Node* head;
    int length;

    /** Initialize your data structure here. */
    MyLinkedList() {
        head = new Node(0);
        length = -1;
    }
    
    /** Get the value of the index-th node in the linked list. If the index is invalid, return -1. */
    int get(int index) {
        if(index>length) return -1;
        Node* cur = head;

        index++;
        while(index--)
        {
            cur = cur->next;
        }
        return cur->val;
    }
    
    /** Add a node of value val before the first element of the linked list. After the insertion, the new node will be the first node of the linked list. */
    void addAtHead(int val) {
        length++;
        Node* newNode = new Node(val);
        newNode->next = head->next;
        head->next = newNode;
    }
    
    /** Append a node of value val to the last element of the linked list. */
    void addAtTail(int val) {
        length++;
        Node* newNode = new Node(val);
        Node* cur = head;
        while(cur && cur->next)
        {
            cur = cur->next;
        } 
        cur->next = newNode;
        

    }
    
    /** Add a node of value val before the index-th node in the linked list. If index equals to the length of linked list, the node will be appended to the end of linked list. If index is greater than the length, the node will not be inserted. */

    void addAtIndex(int index, int val) {
        if(index>length+1)
        {
            return;
        }
        else if(length+1==index)
        {
            addAtTail(val);
            return;
        }
        else if(index==0)
        {
            addAtHead(val);
            return;
        }
        else
        {
            Node* cur = head;
            while(index--)
            {
                cur = cur->next;
            }
            Node* newNode = new Node(val);
            newNode->next = cur->next;
            cur->next = newNode;
            length++;
        }

    }
    
    /** Delete the index-th node in the linked list, if the index is valid. */
    void deleteAtIndex(int index) {
        if(index>length) return;

        Node* cur = head;
        
        while(index--)
        {
            cur = cur->next;
        }
        cur->next = cur->next->next;
        length--;

    }
};

/**
 * Your MyLinkedList object will be instantiated and called as such:
 * MyLinkedList* obj = new MyLinkedList();
 * int param_1 = obj->get(index);
 * obj->addAtHead(val);
 * obj->addAtTail(val);
 * obj->addAtIndex(index,val);
 * obj->deleteAtIndex(index);
 */

14. 复杂链表的复制

【题目】

请实现 copyRandomList 函数，复制一个复杂链表。在复杂链表中，每个节点除了有一个 next 指针指向下一个节点，还有一个 random 指针指向链表中的任意节点或者 null。

【解析】

random指针怎么复制？直接复制就指向原链表的节点了，违背题意，必须让它指向复制出来的节点，那就先把原链表按next指针复制出来，再修复random指针？也不行，原链表random指针指向的是一块内存，我们无法通过原链表的指针来判断新链表指针的指向。我的第一个想法是用数组存储原链表，这样就可以记录每一个节点random指针指向链表中哪个【位置】的节点，然后先用next指针复制原链表，把新链表的节点存储到一个临时数组中，再用我们之前得出的位置信息修复每一个节点的random指针即可。

【ac代码】

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* next;
    Node* random;
    
    Node(int _val) {
        val = _val;
        next = NULL;
        random = NULL;
    }
};
*/
class Solution {
public:
    vector<Node*> tmp;
    vector<int> index;
    vector<Node*> re;
    
    Node* copyRandomList(Node* head) {
        if(!head) return NULL;
        
        Node* cur = head;
        while(cur) //将原链表所有节点存入一个临时数组中，这样就可以通过下标访问节点
        {
            tmp.push_back(cur);
            cur = cur->next;
        }
        int length = tmp.size();
        /*再用一个index数组，记录原链表中每一个节点random指针指向的节点下标*/
        for(int i = 0;i<length;i++)
        {
            if(tmp[i]->random == NULL)
            {
                index.push_back(-1);
                continue;
            }
            for(int j = 0;j<length;j++)
            {
                if(tmp[i]->random == tmp[j]) index.push_back(j); 
            }
        }
        /*将原链表所有节点按序存入数组re中*/
        for(int i = 0;i<length;i++)
        {
            Node* newNode = new Node(tmp[i]->val); 
            re.push_back(newNode);
        }
        /*在数组re中通过index数组提供的位置修复每一个节点的random指针，同时将每个节点用next连接*/
        for(int i = 0;i<length;i++)
        {
            if(index[i] == -1) re[i]->random = NULL;
            else re[i]->random = re[index[i]];
            if(i<length-1) re[i]->next = re[i+1];
        }
        
        return re[0];
    }
};

15. 移除链表元素

【题目】

删除链表中等于给定值 val 的所有节点。

示例:

输入: 1->2->6->3->4->5->6, val = 6
输出: 1->2->3->4->5

【解析】

设置一个哑节点，使得头结点值等于val时的处理方法与普通情况一致。

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        ListNode* dumpyHead = new ListNode();
        dumpyHead->next = head;
        ListNode* cur = dumpyHead;
        while(cur)
        {
            if(cur->next && cur->next->val==val) cur->next = cur->next->next; //如果本次遍历删除了节点，那么cur节点无需后移（因为本身就是判断cur->next->val是否等于目标值，删除已经相当于后移了）
            else cur = cur->next;
        }
        return dumpyHead->next; //有可能删除的是头结点，因此要返回哑节点的next指针
    }
};

16. 两个链表的第一个公共节点

【题目】

输入两个链表，找出它们的第一个公共节点。注意公共节点之前两个链表的子链表不一定等长，且第一个公共节点后全是公共节点。

【解析】

先将第一个链表的所有节点作为key存入hashmap，然后遍历第二个链表，每经过一个节点就去哈希表中寻找是否存在相同。

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        unordered_map<ListNode*, int> hashmap;
        ListNode* cur = headA;
        while(cur) //先将第一个链表的所有节点作为key存入哈希表
        {
            hashmap[cur]++;
            cur = cur->next;
        }
        
        cur = headB;
        while(cur) //遍历第二个链表，每走到一个节点就在哈希表中找相同
        {
            if(hashmap.count(cur)) return cur; //如果有相同的，那么cur就是第一个公共节点
            cur = cur->next;
        }
        return NULL; //两个链表不存在公共节点
    }
};

【解析2】

另外一种比较经典的解法为：让两个指针在各自的链表中遍历，一旦走到自己的链表尾部就退回到【另外一个链表的头部】，每走一步判断两个指针是否相等，如果相等就返回任意一个指针即可。

该方法正确的原因在于，如果两个链表存在公共节点，那么两个指针先第一次遍历完各自的链表，然后退回到对方的链表头重新开始遍历后，它们必然会在第一个公共节点相遇（因为这时走过的节点数相等）；如果两个链表不存在公共节点，那么两个指针必然会在第二次遍历完整个链表的终点NULL处相遇。

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* a = headA;
        ListNode* b = headB;
        while(a!=b)
        {
            if(a==NULL) a = headB;
            else a = a->next;

            if(b==NULL) b = headA;
            else b = b->next;
        }
        return a;
    }
};

【解析3】

还可以先计算两个链表公共节点前的子链表的长度差N，让公共节点前子链表较长的指针先多走N步。有兴趣可以自己实现下。

17. 链表组件

【题目】

给定链表头结点 head，该链表上的每个结点都有一个唯一的整型值。

同时给定列表 G，该列表是上述链表中整型值的一个子集。

返回列表 G 中组件的个数，这里对组件的定义为：链表中一段最长连续结点的值（该值必须在列表 G 中）构成的集合。

【解析】

遍历链表，每遍历一个节点都去列表G中寻找该节点，如果该节点在G中存在，那么开始计算当前组件数量，不断前进判断下一个节点…一直到走到链表某个节点在G中不存在，则【开始计算组件数量时的节点】到【当前节点的上一个节点】形成一个组件；如果该节点不存在G中，前进到下一个节点继续判断。

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    int numComponents(ListNode* head, vector<int>& G) {
        unordered_map<int, int> hashmap;
        int length = G.size();
        for(int i = 0;i<length;i++) hashmap[G[i]]++; //将列表G中所有整数保存到哈希表中（因为查询效率高）

        ListNode* cur = head;
        int count = 0; //计算有多少个组件
        while(cur) //用指针cur遍历链表
        {
            if(hashmap[cur->val]) //如果哈希表中（列表G）中存在链表cur节点的值。
            {
                //令指针cur在链表中一直前进到G中不存在的节点
                while(cur && hashmap[cur->val]) cur = cur->next;
                
                count++; //现在相当于找到一个组件（note：count++一定要放在该条件内，否则G中不存在的节点也会被视为组件。）
            }
            
            if(cur) cur = cur->next; //现在cur指向G中不存在的节点，因此要前进到下一个节点。另外之前cur很可能已经走到NULL了，因此要进行检查
        }
        return count;
    }
};

18. 奇偶链表

【题目】

给定一个单链表，把所有的奇数节点和偶数节点分别排在一起。请注意，这里的奇数节点和偶数节点指的是节点编号的奇偶性，而不是节点的值的奇偶性。

请尝试使用原地算法完成。你的算法的空间复杂度应为 O(1)，时间复杂度应为 O(nodes)，nodes 为节点总数。

【解析】

定义一个奇链表一个偶链表，他们的节点都属于原链表，定义完成后将偶链表接到奇链表尾部即可。

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* oddEvenList(ListNode* head) {
        if(head==NULL || head->next==NULL) return head;
        
        ListNode* odd = head; //奇链表头
        ListNode* even = head->next;//偶链表头
        ListNode* evenHead = even; //偶链表头在后面的操作中会丢失，因此要先保存
        
        while(odd->next && even->next) //用原链表生成奇偶两个链表
        {
            odd->next = even->next;
            odd = odd->next;

            even->next = odd->next;
            even = even->next;
        }
        
        odd->next = evenHead; //将偶链表连接到奇链表尾部
        return head;
    }
};

19. 分割链表

【题目】

给定一个链表和一个特定值 x，对链表进行分隔，使得所有小于 x 的节点都在大于或等于 x 的节点之前。

你应当保留两个分区中每个节点的初始相对位置。

示例:

输入: head = 1->4->3->2->5->2, x = 3
输出: 1->2->2->4->3->5

【解析】

设置两个头little和big，一个专门指向比x小的节点，另一个指向大于等于x的节点，然后遍历原链表，将相应的节点连接到对应的头上，最后拼接即可。本题能深切的体会到使用哑节点的好处。

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* partition(ListNode* head, int x) {
        ListNode* little = new ListNode(); //little哑节点
        ListNode* big = new ListNode();    //big哑节点
        
        ListNode* saveBig = big;
        ListNode* saveLittle = little;
        ListNode* cur = head;
        
        while(cur)
        {
            if(cur->val<x)
            {
                little->next = cur;
                little = little->next;
            }
            else
            {
                big->next = cur;
                big = big->next;
            }
            cur = cur->next;
        }
        
        big->next = NULL; //防止环路
        little->next = saveBig->next;//将big接到little尾部
        return saveLittle->next;//返回little头节点
    }
};

20. 分隔链表

【题目】

给定一个1~50的整数k，将链表分为k个子链表，其中任意两个子链表的长度差不超过1，且左边的子链表长度总是【大于等于】右边子链表的长度。

【解析】

根据提示，定义链表长度为N，则前N%k个子链表长度为N/k+1，后面所有子链表长度为N/k。

两遍遍历链表，第一遍获取总长度，第二遍按照上述规律在原链表上直接分隔链表，要注意的是每分隔完一个子链表要记录下一个节点，并把这个分隔完的子链表的最后一个节点next指针置为NULL，然后从记录的下一个节点开始继续分隔下一个子链表。

【ac代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    vector<ListNode*> splitListToParts(ListNode* root, int k) {
        vector<ListNode*> re;
        ListNode* cur = root;
        int length = 0;  //链表总节点数

        while(cur)//第一次遍历，获取链表长度
        {
            length++;
            cur = cur->next;
        }
        
        int everyPart = length/k; //每一个子链表的【预估】长度
        int extraPart = length%k;//前extraPart个子链表长度要加1

        int partCount = 0; //记录当前分隔到第几个子链表
        ListNode* save = root; //用来保存下一个子链表的头节点
        int loop = 0; //每个子链表的【实际】长度
        
        cur = root;
        while(cur) //第二次遍历原链表，进行分隔操作
        {
            cur = save; //上一次save的节点就是当前子链表的头节点
            if(save) re.push_back(save); //将当前子链表放入答案数组
            
		   /*计算当前子链表的实际分隔长度，前extraPart个子链表长度要多1*/
            if(partCount<extraPart) loop = everyPart;
            else loop = everyPart-1;

			//该循环结束后cur所在位置就是当前子链表尾部
            for(int i = 0;i<loop && cur;i++) cur = cur->next; 

            if(cur)
            {
                save = cur->next; //保存当前子链表尾部的下一个节点，即下一个子链表的头结点
                cur->next = NULL; //截断当前子链表尾部
                partCount++;      
            }
        }
        
        /*如果链表分隔完成后，子链表数量还小于k，继续塞空指针*/
        while(partCount<k) 
        {
            re.push_back(NULL);
            partCount++;
        }
        return re;
    }
};