《数组》专题

Posted on Edited on In , Views:

1. 将有序数组中所有元素平方

【题目】

Given an array of integers A sorted in non-decreasing order, return an array of the squares of each number, also in sorted non-decreasing order.

Example 1:

Input: [-4,-1,0,3,10]
Output: [0,1,9,16,100]

Example 2:

Input: [-7,-3,2,3,11]
Output: [4,9,9,49,121]

【解析】

普通做法：先对所有元素平方，然后排序。时间复杂度O(n+nlogn)

双指针做法：利用题目条件。题目给定的数组是单调不减的数组，因此可以先找到一个seperator（其左侧元素全负，右侧元素全正），然后将整个数组所有元素平方。这时从（seperator-1，0）是一个单调递减的数组，从（seperator，arrayLength-1）是另一个单调递减的数组，将它们归并排序。此法的时间复杂度为O(n)。

【ac代码】

双指针做法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    vector<int> sortedSquares(vector<int>& A) {
        int seperator = 0; //数组中正负的分界点
        int length = A.size();
        vector<int> re;
        
        for(int i = 0;i<length;i++) //寻找分界点
        {
            if(A[i]>=0) 
            {
                seperator = i;
                break;
            }
        }

        for(int i = 0;i<length;i++) A[i]*=A[i]; //将整个数组平方

		/*归并排序*/
        int l = seperator-1, r = seperator, k = 0;
        while(l>=0&&r<length)
        {
            if(A[l]<A[r]) re.push_back(A[l--]);
            else re.push_back(A[r++]);
        }
        while(l>=0) re.push_back(A[l--]);
        while(r<length) re.push_back(A[r++]);
        return re;
        
    }
};

2. 数组中有多少比当前元素少的数

【题目】

Given the array nums, for each nums[i] find out how many numbers in the array are smaller than it. That is, for each nums[i] you have to count the number of valid j’s such that j != i and nums[j] < nums[i].

Return the answer in an array.

Example 1:

Input: nums = [8,1,2,2,3]
Output: [4,0,1,1,3]
Explanation:
For nums[0]=8 there exist four smaller numbers than it (1, 2, 2 and 3).
For nums[1]=1 does not exist any smaller number than it.
For nums[2]=2 there exist one smaller number than it (1).
For nums[3]=2 there exist one smaller number than it (1).
For nums[4]=3 there exist three smaller numbers than it (1, 2 and 2).

Example 2:

Input: nums = [6,5,4,8]
Output: [2,1,0,3]

Example 3:

Input: nums = [7,7,7,7]
Output: [0,0,0,0]

Constraints:

2 <= nums.length <= 500
0 <= nums[i] <= 100

《暴力法》

【解析】

对数组中每一个元素都遍历一遍整个数组，找出所有比它小的数。

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<int> smallerNumbersThanCurrent(vector<int>& nums) {
        int length = nums.size();
        vector<int> re;
        int count; //记录数组中有多少个元素比nums[i]小
        for(int i = 0;i<length;i++)
        {
            count = 0;
            for(int j = 0;j<length;j++) 
            {
                if(nums[j]!=nums[i] && nums[j]<nums[i]) count++;
            }
            re.push_back(count);
        }
        return re;
    }
};

《木桶法》

【解析】

注意到题目说明了数据范围，数组中每个元素都小于100。因此可以创建100个桶，把元素（整数）放入下标与其相等的桶中，完成后再遍历原数组（因为答案要求与原数组同序），比nums[i]小的元素数量就是0~i-1号桶（有记录的情况下）记录的频率总数。

这解法告诉我们，一定要认真读题！！！

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
private:
    int barrel[101]={0}; //要开到101个位置，数组的最大下标才为100
    vector<int> re;
    
public:
    vector<int> smallerNumbersThanCurrent(vector<int>& nums) {
        int length = nums.size();
        for(int i = 0;i<length;i++) //把元素出现频率记录在桶中
        {
           barrel[nums[i]]++;
        }
        
        //重新遍历原数组，计算对于每一个元素，数组中比它小的元素有多少
        int sum = 0;
        for(int i = 0;i<length;i++)
        {
            sum = 0;
            //比nums[i]小的元素数量为sum(barrel[0]~barrel[i-1])
            for(int j = 0; j<nums[i]; j++) sum += barrel[j];
            re.push_back(sum);
        }
        return re;
    }
};

3. 奇偶排序数组

【题目】

给定一个非负整数数组 A， A 中一半整数是奇数，一半整数是偶数。

对数组进行排序，以便当 A[i] 为奇数时，i 也是奇数；当 A[i] 为偶数时， i 也是偶数。

你可以返回任何满足上述条件的数组作为答案。

提示：

  1. 2 <= A.length <= 20000
  2. A.length % 2 == 0
  3. 0 <= A[i] <= 1000

【解析】

双指针法，在原数组中使用一个奇指针（ji）和一个偶指针（ou），奇偶指针所指的元素轮流push到答案数组中即可。

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<int> sortArrayByParityII(vector<int>& A) {
        vector<int> re;
        int length = A.size();
        int ji = 0, ou = 0;
        while(ou<length && ji<length)
        {
            while(ou<length && A[ou]%2!=0) ou++; //寻找下一个偶元素所在位置
            re.push_back(A[ou++]);

            while(ji<length && A[ji]%2==0) ji++; //寻找下一个奇元素所在位置
            re.push_back(A[ji++]);
        }
        return re;
    }
};

4. 区间合并

将所有存在交集的区间合并为一个区间。

如[1,2,3]、[3,4,5]合并为[1,2,3,4,5,]

这类问题一般是先将所有区间按照左端点排序

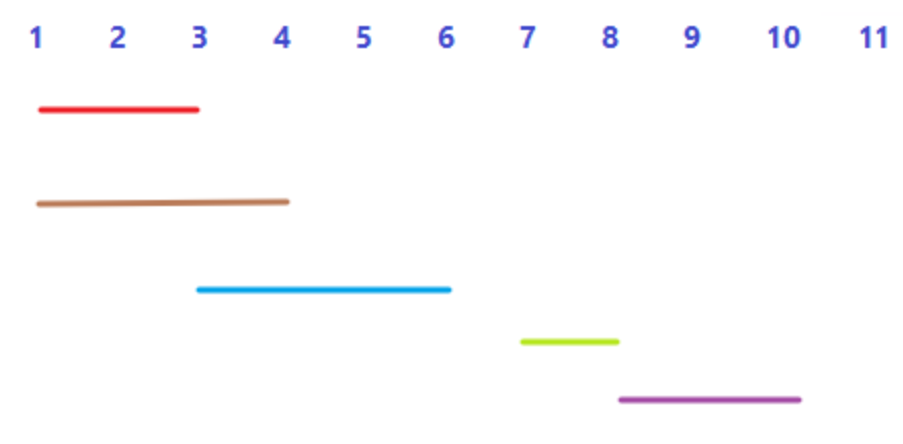
然后逐个判断是否存在交集。（要注意的是有些区间的右端点可能比它的下一个区间的右端点大）

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
​```C++

typedef pair<int, int> PII; //自定义二元组类型
vector<PII> merge(vector<PII>& arr)
{
    vector<PII> re;//存放已经合并好的数组
    sort(arr.begin(),arr.end());//按每个区间最左侧端点排序
    
    for(int i = 0;i<arr.size()-1;i++)
    {
          while(i<arr.size()-1&&arr[i].second>=arr[i+1].first)//如果当前区间和下个区间重合 
         {
                if(arr[i].second>arr[i+1].second) //如果当前区间最右侧位置大于下一区间最右侧位置
                {//令下一区间等于当前区间
                     arr[i+1].first = arr[i].first;
                     arr[i+1].second = arr[i].second;
                }
                else//如果当前区间最右侧位置小于下一区间最右侧位置
                {//把下一区间的左端点拉伸到当前区间的左端点位置
                    arr[i+1].first = arr[i].first;    
                }
                i++; //继续判断合并后的区间是否与它的下一区间重合
         }
         re.push_back(arr[i]);
     }
     return re;
 }
​```

4.1 区间合并模板题

以【左端点，右端点】的形式给出一组区间，将这组区间合并，求出合并后的区间数量。（注：两区间端点相交也算重合）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
typedef pair<int, int> PII;
vector<PII> ve;  //其中每一个元素都代表一个区间的两个端点下标

/*将所有存在交集的区间合并，返回合并后的区间集合*/
vector<PII> IntervalMerge(vector<PII>& value)
{
    vector<PII> re; //返回值
    sort(value.begin(), value.end()); //将所有区间按照左端点大小排序
    
    
    for(int i = 0;i<value.size()-1;i++)//遍历所有区间
    {
        //如果当前区间和下一个区间重合
        while(i<value.size()-1&&value[i].second>=value[i+1].first) 
        {
            
            /*将下一区间变为当前区间*/
            //如果当前区间包含下一个区间
            if(value[i].second>=value[i+1].second)
            {
                value[i+1].first = value[i].first;
                value[i+1].second = value[i].second;
            }
            
            //如果当前区间不包含下一个区间
            else
            {
                value[i+1].first = value[i].first;
            }
            i++; //继续检查合并后的区间能否与它的下一个区间合并
        }
        re.push_back(value[i]);
    }
    return re;
}

int main()
{
    int n;
    scanf("%d",&n);
    int a,b;
    for(int i = 0;i<n;i++) 
    {
        scanf("%d%d",&a,&b);
        ve.push_back({a,b});
    }
    vector<PII> re = IntervalMerge(ve);
    printf("%d",re.size());
    return 0;
}

5. 前缀和

前缀和的作用就是能快速地（在O(1)时间内）求出数组某子集的和，因此当问题多次询问数组某一区间（每次不同）的和时首先考虑用前缀和。

5.1 一维前缀和

原数组（差分）：$a_1a_2a_3a_4…a_i$

前缀和数组: $S_i=a_1+a_2+a_3+…+a_i=S_{i-1}+a_{i}$

求某子集的和: $Sum[l,r]=s_r-s_{l-1}$

定义$S_0=0$，且定义原数组a下标从1开始（为了统一格式）。
因为假如我们要求和的子集下标下界刚好为最小下标处（即下标1处）时，$S_{l-1}$才有意义，使得整个公式统一了。

模板

  1. 先初始化前缀和数组（假设给定下标从0开始的数组是arr[ ], 且定义好s[0]=0，求arr[]的前缀和数组s[]）
    1
    2
    /*原数组arr的下标从1开始*/
    for(int i = 1;i<=arr.size();i++) s[i] = s[i-1]+arr[i];
  2. 得到前缀和数组后，对于每次对原数组区间[l, r]的和的询问，只需要做一个减法：s[r]-s[l-1]就行了。（如求[1, 2]、[5, 8]子集的和）

[1,2]子集的和 = s[2]-s[0];

[5,8]子集的和 = s[8]-s[4];

5.1.1 一维前缀和模板题

【题目】

https://www.acwing.com/problem/content/797/

输入一个长度为n的整数序列。

接下来再输入m个询问，每个询问输入一对l, r。

对于每个询问，输出原序列中从第l个数到第r个数的和。

输入格式

第一行包含两个整数n和m。

第二行包含n个整数，表示整数数列。

接下来m行，每行包含两个整数l和r，表示一个询问的区间范围。

输出格式

共m行，每行输出一个询问的结果。

数据范围

1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000

输入样例：

1
2
3
4
5
5 3
2 1 3 6 4
1 2
1 3
2 4

输出样例：

1
2
3
3
6
10

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<iostream>
using namespace std;
const int N = 100010;
int q[N];
int s[N];

int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i = 1;i<=n;i++) scanf("%d",&q[i]);
    for(int i = 1;i<=n;i++) s[i] = s[i-1]+q[i];
    
    int l, r;
    while(m--)
    {
        scanf("%d%d",&l,&r);
        printf("%d\n", s[r]-s[l-1]);
    }
    return 0;
}

5.2 二维前缀和

二位前缀和的作用是快速求矩阵（长宽可不等）中某一子矩阵中所有元素的和。

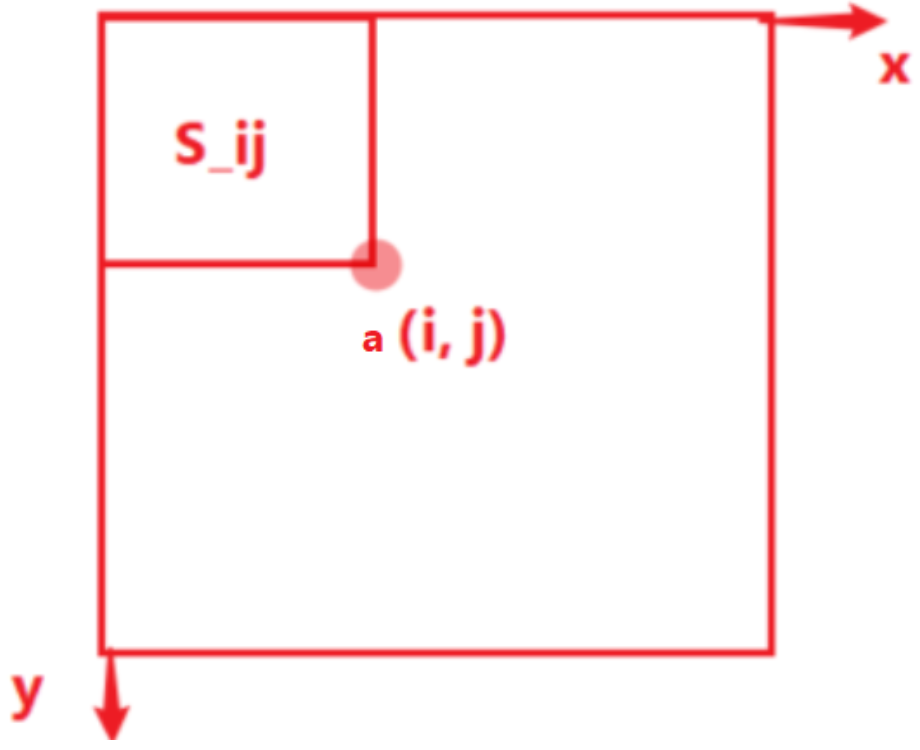
在矩阵a中，$S_{ij}$就表示以$(0, 0)$为左上角，$a(i, j)$为左下角的子矩阵中所有元素的和。

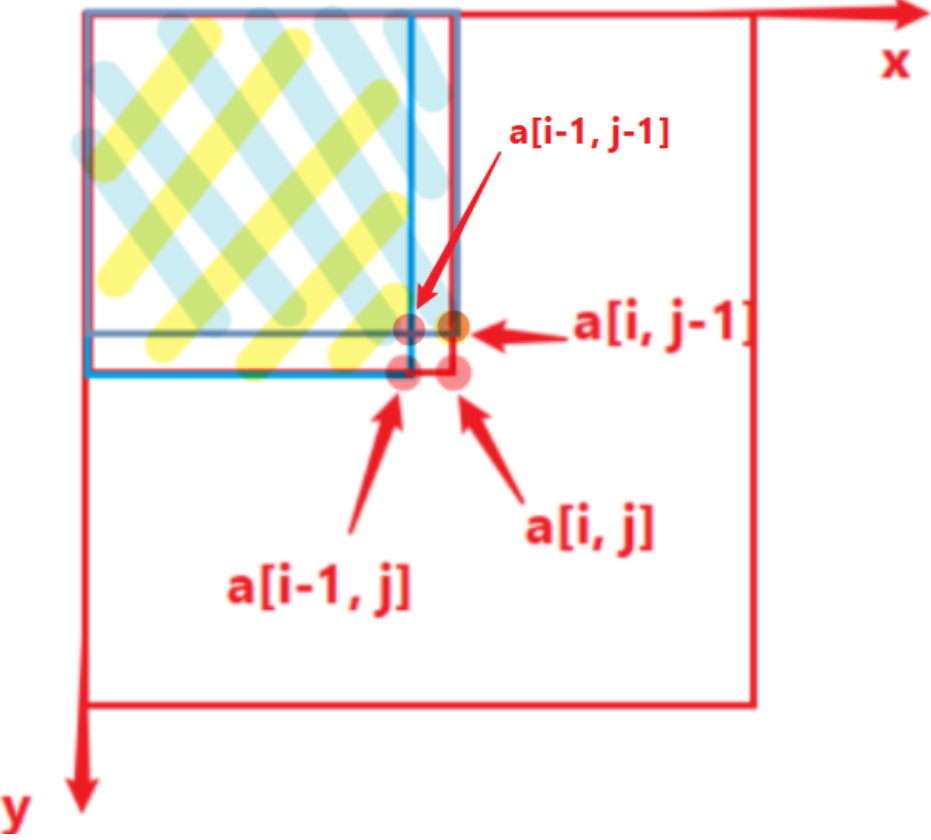
$S_{ij}$可以这样计算：
$$
S_{ij} = S_{(i-1)j}+S_{i(j-1)}-S_{(i-1)(j-1)}+a_{ij}
$$

通过这个公式，就可以构造出矩阵a的前缀和矩阵S。

1
2
3
for(int i = 1;i<n;i++)
    for(int j = 1;j<m;j++)
        s[i][j] = s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];

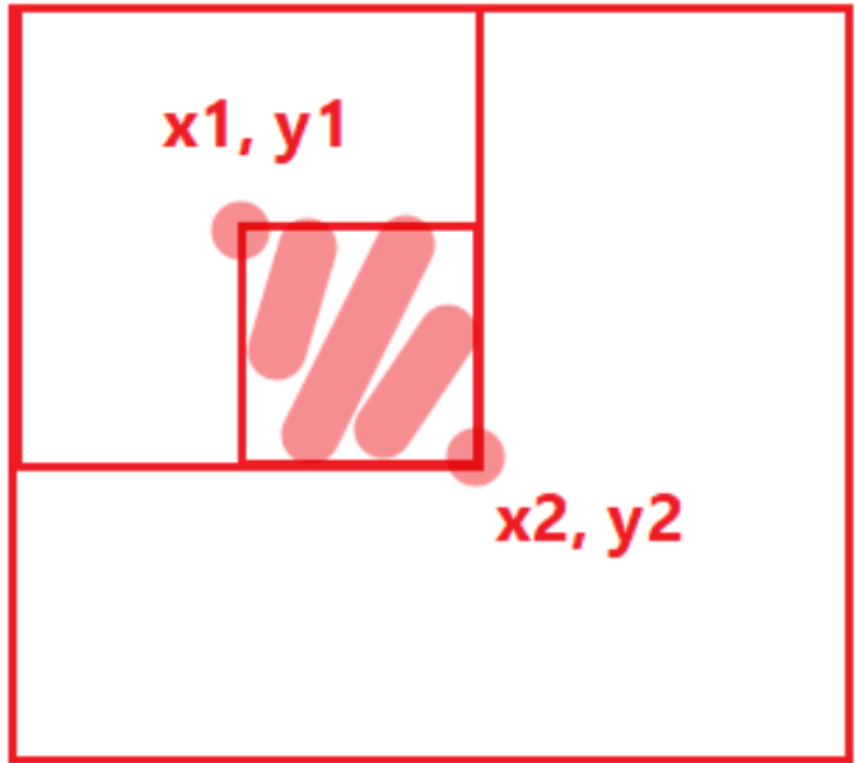
之后的询问给出矩阵a中任一子矩阵的左上角坐标(x1, y1)和右下角坐标(x2, y2)，我们就可以通过4次加减运算快速求出a矩阵中任一子矩阵所有元素的和：


$$
sum = s[x_2][y_2]-s[x_1-1][y_2]-s[x_2][y_1-1]+s[x_1-1][y_1-1]
$$

5.2.1 二维前缀和模板题

【题目】

https://www.acwing.com/problem/content/798/

输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式

第一行包含三个整数n，m，q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含四个整数x1, y1, x2, y2，表示一组询问。

输出格式

共q行，每行输出一个询问的结果。

数据范围

1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<iostream>
using namespace std;
const int N = 1010;
int d[N][N];
int s[N][N];


int main()
{
    int n,m,q;
    scanf("%d%d%d",&n,&m,&q);
    for(int i = 1;i<=n;i++)
    {
        for(int j = 1;j<=m;j++)
        {
            scanf("%d",&d[i][j]);
            s[i][j] = s[i-1][j]+s[i][j-1]-s[i-1][j-1]+d[i][j];
        }
    }
    
    int x1,y1,x2,y2;
    while(q--)
    {
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        printf("%d\n",s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]);
    }
    return 0;
}

6. 差分

求差分就是求前缀和的逆运算，它的作用是快速的对数组的某子数组中所有元素进行加减运算。

6.1 一维差分

回顾前缀和的定义：

原数组（差分）：$a_1a_2a_3a_4…a_i$

前缀和：$S_i = a_1+a_2+…+a_i=S_{i-1}+a_i$

因此差分的定义就是

给定一个数组：$S_1S_2S_3S_4…S_i$

它的差分数组d[ ]满足：$S_r = d_1+d_2+…+d_r$

这样一来，如果我们要对数组S的某一子集中所有元素进行加减操作，可以先构造到这个数组S的差分数组d。假设对差分数组中元素$d_5$加上5，则把复原为原数组后，原数组$S_5$和$S_5$之后的所有元素都被加上了5（因为$S_5$和$S_5$之后的所有元素都有一个共同的加数$d_5$）。但这只对$S_5$和$S_5$之后的所有元素生效，如果不光定义了左边界还定义了右边界呢？

例如想要对S数组的[l,r]这个区间内所有元素+10，那就先构造它的差分数组d，然后执行$d_l+10$, 再执行$d_{r+1}-10$即可。（相当于先把$S_l$和$S_l$之后的所有元素+10，然后把$S_r$之后的所有元素-10），然后再求差分数组d的前缀和（即复原），就得到[l, r]区间所有元素+10后的S数组了。

怎么根据现有数组来构造它的差分数组呢？

首先可以确定的是全0数组的差分数组也一定是全零的。利用这一点，在判断“多次对数组不同区间的扫描中，某一下标位置被扫描的次数“这类问题时，可轻松利用差分求出。

而对于非全0的数组：

  1. 假设差分数组为d，它的前缀和数组（也就是原数组）为S。
    我们知道它们有这样一种关系：$d[i] = S[i]-S[i-1]$
    这样一来我们就能构造出任意数组的差分数组了。
  2. 另外还可用插入法构造差分数组（推荐）。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    void insert(int l, int r, int c)
    {
        d[l] += c;
        d[r + 1] -= c;
    }
    for (int i = 1; i <= n; i++) 
    {   
        insert(i, i, S[i]);
    }

6.1.1 一维差分模板题

【题目】

https://www.acwing.com/problem/content/799/

输入一个长度为n的整数序列。

接下来输入m个操作，每个操作包含三个整数l, r, c，表示将序列中[l, r]之间的每个数加上c。

请你输出进行完所有操作后的序列。

输入格式

第一行包含两个整数n和m。

第二行包含n个整数，表示整数序列。

接下来m行，每行包含三个整数l，r，c，表示一个操作。

输出格式

共一行，包含n个整数，表示最终序列。

数据范围

1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<iostream>
using namespace std;
const int N = 100010;
int d[N];
int s[N];

void insert(int l, int r, int c) 
{
    d[l] += c;
    d[r+1] -= c;
}

int main()
{
    int n, m;
    scanf("%d%d",&n,&m);
    
    for(int i = 1;i<=n;i++)
    {
        scanf("%d",&s[i]); 
        insert(i, i, s[i]); //根据s[]构造差分数组
    }
    
    int l, r, val; //将原数组区间[l, r]中所有的元素加val
    while(m--)
    {
        scanf("%d%d%d",&l,&r,&val);
        insert(l, r, val); 
    }
    
    for(int i = 1;i<=n;i++) s[i] = s[i-1]+d[i]; //将差分数组复原成原数组
    for(int i = 1;i<=n;i++) printf("%d ",s[i]);
    return 0;
    
}

6.2 二维差分

与一维类似，它目的是快速地对矩阵的某子矩阵中所有的元素进行加减操作。

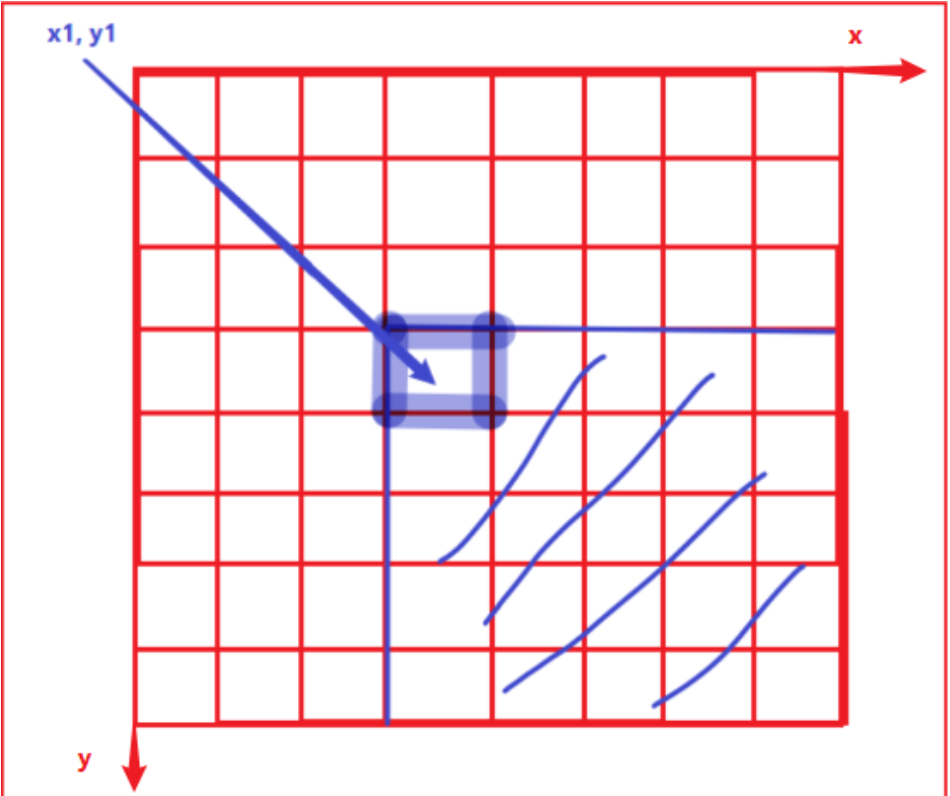
如上图矩阵d，把$(x_1, y_1$)这个点上的值加上或者减去x，则d的前缀和矩阵中所有位于点$(x_1, y_1)$（包括它本身）右下角的值全部加上或者减去x。

因此，当需要多次对矩阵s中不同的子矩阵中所有元素进行加减操作时，可以先根据s构造出它对应的差分数组d，然后对d进行上图中的操作，最后再求出d的前缀和数组，这个前缀和数组就是对s中某一子矩阵中所有元素进行了加减操作后的数组。

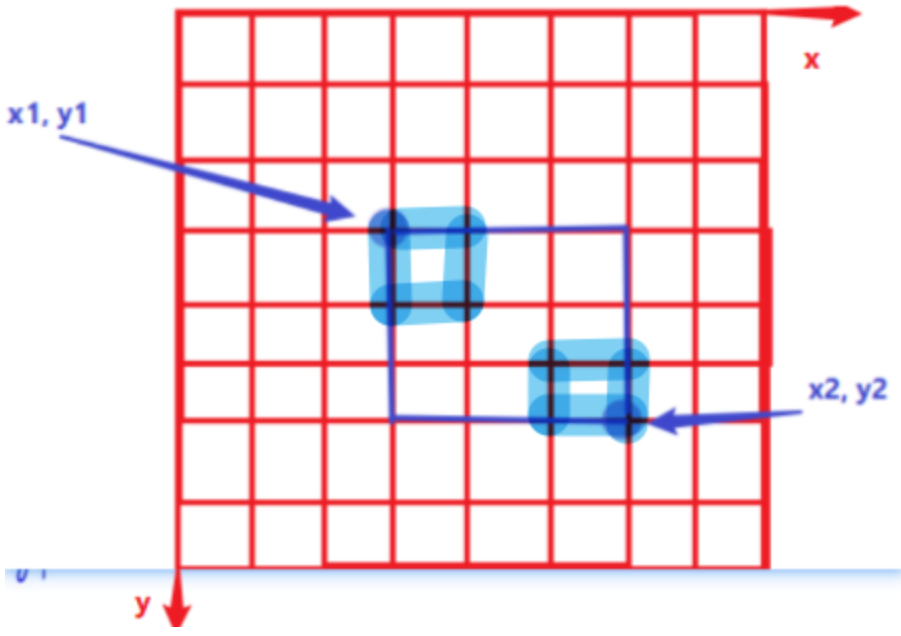
举个例子，假如现在我们要把上图矩阵s的蓝色区域中所有元素+val：

第一步，通过插入法构造差分矩阵（构造好的矩阵d也如上图）

1
2
3
4
5
6
7
8
9
10
void insert(int x1, int y1, int x2, int y2, int val) {
    d[x1][y1] += val;
    d[x2 + 1][y1] -= val;
    d[x1][y2 + 1] -= val;
    d[x2 + 1][y2 + 1] += val;
}
    
for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            insert(i, j, i, j, S[i][j]);

第二步，进行如下步骤对d矩阵进行操作（每进行一轮如下操作，相当于将原矩阵中由【左上角(x1, y1)和右下角(x2, y2)】确定的子矩阵中所有元素加上val）

  • $d(x_1, y_1) +=val$
  • $d(x_1, y_2+1) -=val$
  • $d(x_2+1, y_1) -=val$
  • $d(x_2+1, y_2+1) +=val$

也就是说，通过二维差分，只需要4次加减运算就可以对某矩阵的任一子矩阵中所有元素同时进行加减运算。

最后一步，计算出d的前缀和数组即可。

6.2.1 二维差分模板题

【题目】

https://www.acwing.com/problem/content/800/

输入一个n行m列的整数矩阵，再输入q个操作，每个操作包含五个整数x1, y1, x2, y2, c，其中(x1, y1)和(x2, y2)表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上c。

请你将进行完所有操作后的矩阵输出。

输入格式

第一行包含整数n,m,q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含5个整数x1, y1, x2, y2, c，表示一个操作。

输出格式

共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围

1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<iostream>
using namespace std;
const int N = 1010;
int d[N][N];
int s[N][N];

void insert(int x1, int y1, int x2, int y2, int val) //插入法构造差分矩阵
{
    d[x1][y1]     += val;
    d[x2+1][y1]   -= val;
    d[x1][y2+1]   -= val;
    d[x2+1][y2+1] += val;
}

int main()
{
    int n,m,q;
    scanf("%d%d%d",&n,&m,&q);
    for(int i = 1;i<=n;i++) //读取原矩阵并构造其对应的差分矩阵
    {
        for(int j = 1;j<=m;j++)
        {
            scanf("%d",&s[i][j]);
            insert(i, j, i, j, s[i][j]);
        }
    }
    
    int x1,y1,x2,y2,c;
    while(q--) //按题目要求对差分矩阵进行操作
    {
        scanf("%d%d%d%d%d", &x1,&y1,&x2,&y2,&c);
        insert(x1,y1,x2,y2,c);
    }
            
    
    for(int i = 1;i<=n;i++) //将差分矩阵恢复为前缀和矩阵
    {
        for(int j = 1;j<=m;j++)
        {
            s[i][j] = s[i-1][j]+s[i][j-1]-s[i-1][j-1]+d[i][j];
            printf("%d ", s[i][j]);
        }
        printf("\n");
    }
    
    return 0;
    
}

7. 矩阵遍历

矩阵遍历是一类问题，如果按照传统方法做，需要大量的if判断出否出界，可以按照如下方法简化：

定义两个方向数组：int dx[] = {-1, 0, 1 ,0}, dy[] = {0, 1, 0, -1};

再定义一个方向$d\in [0,3]$ ，那么如果指针当前遍历到矩阵的[x, y]处：

  1. 向上走（d=1方向）: x+=dx[d], y+=dy[d]。完成后指针移动到[x, y+1]处。
  2. 向右走（d=2方向）: x+=dx[d], y+=dy[d]。完成后指针移动到[x+1, y]处。
  3. 向下走（d=3方向）: x+=dx[d], y+=dy[d]。完成后指针移动到[x, y-1]处。
  4. 向左走（d=0方向）: x+=dx[d], y+=dy[d]。完成后指针移动到[x-1, y]处。

可以看到，只需要改变d的值即可完成4个方向移动的操作，而且采用该方法后判断指针是否越界十分方便。另外，该方法可以很轻易的拓展为其他情况，比如往一个点周围的8个方向走，看到这里请读者尝试构造出8个方向的方向数组。

7.1 顺时针打印矩阵

这是上述方案的典型应用。

【题目】

https://leetcode-cn.com/problems/shun-shi-zhen-da-yin-ju-zhen-lcof/

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector<int> re;
        int row = matrix.size();
        if(row==0) return re;
        int column = matrix[0].size();
        
        int dx[] = {-1, 0, 1 ,0}, dy[] = {0, 1, 0, -1}; //方向数组
        int x = 0, y = 0, d = 1; //从(0, 0)开始走，初始方向d=1（即向右走一步）
        for(int i = 0;i<row*column;i++){
            re.push_back(matrix[x][y]);
            matrix[x][y] = 0x3f3f3f3f; //走过的点要标记一下
            int a = x+dx[d], b = y+dy[d]; //下一个到达的位置是(a, b)
            if(a<0 || a>=row || b<0 || b>=column || matrix[a][b] == 0x3f3f3f3f){ //如果(a, b)这个坐标越界，或者(a, b)已经被访问过
                d = (d+1)%4; //改变方向
                a = x+dx[d], b = y+dy[d]; ////下一个到达的位置是(a, b)
            }
            x = a, y = b; //指针继续走
        }
        return re;
    }
};

8. 双指针

最…子数组这类问题一般都可以暴力做出来，然后利用双指针降低复杂度，其关键在于抓住题目条件挖掘出数组的一些性质从而将问题通过一次遍历解决掉。

8.1 连续子数组的最大和

【题目】

https://leetcode-cn.com/problems/lian-xu-zi-shu-zu-de-zui-da-he-lcof/

在一个存在负数的数组中找出和最大的子数组，返回这个和。

【解析】

将子数组想象成一个不断向右侧扩大的窗口，一开始窗口中只包含数组的第一个元素。每次窗口右端点扩大前，先检查当前窗口的和，如果和为负数，那么当前窗口必然不会出现在和最大的连续子数组中，所以这时应该将窗口左端点向右收缩到与右端点扩大后相同的位置。多次求某窗口的和可以先预处理出前缀和提高速度。

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int maxSubArray(int[] nums) {
        int[] sum = new int[nums.length+1];
        for(int i = 0;i<nums.length;i++) sum[i+1] = sum[i] + nums[i]; //前缀和

        int left = 1;
        int mx = Integer.MIN_VALUE;
        for(int right = 1;right<sum.length;right++){
            int intervalSum = sum[right]-sum[left-1]; //当前窗口的和
            mx = Integer.max(mx, intervalSum);        //取窗口和的最大值
            if(intervalSum<0) { 					//如果当前窗口和小于0，将窗口收缩到与其右端点扩大后相同的位置
                left = right+1;
            }
        }
        return mx;
    }
}