《排序》专题

Posted on Edited on In , Views:

1. 插入排序

1.1 直接插入排序

适用于数据基本有序且数据量不大的数组。

思想：假定前i个元素有序，每次排序将第i+1个元素插入到有序部分中（采用比较和交换位置的方法），使得前i+1个元素有序

代码：

1
2
3
4
5
6
7
8
9
10
void InsertSort(int* a, int length)
{
    for(int i = 1;i<length;i++) //第1个元素直接有序，从第2个元素开始
    {
        for(int j = i;j>0;j--)  //将第i个元素插入到前(i-1)个元素中，使0~i有序
        {
            if(a[j]<a[j-1]) swap(a[j], a[j-1]);
        }
    }
}

分析
时间复杂度：平均$O(n^2)$，最好$O(n)$，最坏$O(n^2)$
空间复杂度：$O(1)$
稳定性：稳定

1.2 折半插入排序

基于直接插入排序，既然每次都假定前i个元素有序，那么查找第i+1个元素插入到这个有序数组中适当位置的方法，就可以采用折半查找。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void LogInsertSort(int* a, int length)
{
    for(int i = 1;i<length;i++) //第1个元素直接有序，从第2个元素开始
    {
        int temp = a[i]; //先将第i个元素缓存起来
        
        /*二分查找，找到a[i]应该放在的第l个位置*/
        int l = 0, r = i;
        while(l < r)
        {
            int mid = (l+r)/2;
            if(a[mid]>temp) r = mid;
            else l = mid+1;
        }
        
        /*将l到i的所有元素后移一格，并把a[i]放到位置l上*/
        for(int j = i; j>l; j--) a[j] = a[j-1]; 
        a[l] = temp;
    }
}

分析
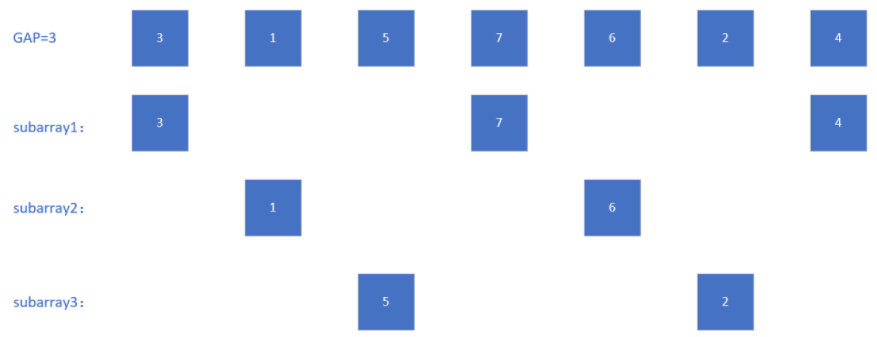
时间空间复杂度与稳定性均与直接插入排序相同，因为总的移动次数不变。实际使用上会比直接插入排序快一些，因为查找速度相对较快。

1.3 希尔排序

插入排序当数组规模较小且数组基本有序时速度很快，但数组基本有序的情况很少见。希尔排序的原理就是不断的使数组整体更加有序，最后再通过一次插入排序得以在很快的时间内使得数组完全有序。

实现: 选定一个gap，将数组按间隔gap划分为gap个子数组。

然后对每一个子数组进行插入排序。
然后gap/=2，重复以上动作，直到最后gap=1，进行一次完全的插入排序，结束。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void HellSort(int* a, int length)
{
    for(int gap = length/2; gap>0; gap/=2)//确定gap
    {
        for(int i = 0; i<=gap; i++)//确定子数组起始位置
        {
            /*对子数组进行插入排序*/
            for(int j = i+gap; j<length; j+=gap)
            {
                for(int k = j; k>=i+gap; k-=gap)
                {
                    if(a[k]<a[k-gap]) swap(a[k], a[k-gap]);
                }
            }
        }
    }
}

分析
时间复杂度：平均$O(n^{1.3})$，最好$O(n)$，最坏$O(n^2)$
空间复杂度：O(1)
稳定性：不稳定

希尔排序是第一批突破$O(n^2)$的算法。因为排序算法的根本原理是消除数组中的逆序对，可以看到$O(n^2)$的算法一般每次迭代只能消除一对逆序对，而希尔排序由于跨度大，每次迭代可能消除多对逆序对，这也是它能突破$O(n^2)$的原因。

2. 交换排序

2.1 冒泡排序

从头到尾步进，碰到逆序对就交换位置，这样每一轮遍历都可以确定末尾元素的位置，进行n轮即可。

1
2
3
4
5
6
7
8
9
10
void BubbleSort(int* a, int length)
{
    for(int i = 0;i<length;i++)
    {
        for(int j = 1;j<length-i;j++)
        {
            if(a[j]<a[j-1]) swap(a[j], a[j-1]);
        }
    }
}

时间复杂度：平均$O(n^2)$，最好$O(n)$，最坏$O(n^2)$
空间复杂度：O(1)
稳定性：稳定

2.2 快速排序

  1. 确定分界点。在数组中随便取一个值，作为pivot
  2. 调整区间。使得pivot左边的值≤pivot，pivot右边的值≥pivot
  3. 按照上面两步递归处理左右两端

难点在于第二步，有两种做法：

  1. 暴力法（需要额外空间）
    创建一个数组a[ ]一个数组b[ ]，扫描arr[ ]，把≤pivot的放入a[ ]，把≥pivot的放入b[ ]。
    然后把a[ ]和b[ ]分别放入arr[ ]。
  2. 双指针（不需要额外空间）
    左右各一指针 l，r 往中间移动。从l开始，它右移的过程中一旦碰到arr[l] >pivot， 就停下，换r行动，它左移的过程一旦碰到arr[r]<pivot，停下，交换arr[l]和arr[r]，换l行动，重复以上步骤，直到 l和r 相遇。
1
2
3
4
5
6
7
8
9
10
11
12
void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;
    int i = l - 1, j = r + 1, pivot = q[l + r >> 1];
    while (i < j)
    {
        do i ++ ; while (q[i] < pivot);
        do j -- ; while (q[j] > pivot);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);  //j替换成i会产生边界问题
}

时间复杂度：平均$O(nlogn)$，最好$O(n)$，最坏$O(n^2)$
空间复杂度：$O(logn)$
稳定性：不稳定

2.2.1 快速选择（快排应用）

它是快速排序的变形，通常用于寻找未排序的数组中第k大的数。
它快的原因是它并不需要像快排那样每次需要递归寻找两边，而是每次仅仅往一边找即可, 因此时间复杂度是

也就是O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int quick_find(int l, int r, int k, int q[])
{
    if (l == r) return q[l];    //如果区间缩小为1，就找到了
    /*快排*/
    int i = l - 1;
    int j = r + 1;
    int pivot = q[i + j >> 1];
    while (i < j)
    {
        do i++; while (q[i] < pivot);
        do j--; while (q[j] > pivot);
        if (i < j) swap(q[i], q[j]);
    }
    
    int leftLength = j - l + 1;   //获取pivot左半边数组长度
    //如果k位于pivot左边，则接下来只需要递归左半边寻找
    if (leftLength >= k) return quick_find(l, j, k, q);
    /*如果k位于pivot右边，则接下来递归右半边寻找，注意要令k=k-leftLength，也就是寻找右半边数组第k-leftLength大的元素*/
    else return quick_find(j + 1, r, k - leftLength, q);
}

3. 选择排序

3.1 简单选择排序

i从头开始，每次在i~length-1中找一个最小元素，与i位置的元素交换位置，i++。即每次可以确定位置i的元素，进行n次即可。

1
2
3
4
5
6
7
8
9
10
11
12
void sort(int q[], int length)
{
    for(int i = 0;i<length;i++)
    {
        int min = i;
        for(int j = i+1;j<length;j++)
        {
            if(q[min]>q[j]) min = j;
        }
        swap(q[i], q[min]);
    }
}

分析
时间复杂度：平均$O(n^2)$，最好$O(n^2)$，最坏$O(n^2)$
空间复杂度：$O(1)$
稳定性: 不稳定

3.2 堆排序

把原数组初始化为大根堆，然后不断执行取出堆顶元素的操作（交换堆顶堆尾元素，然后整体size–固定堆尾元素，接着把新的结构“堆化”）。当size=0的时候，整个数组就变成升序。(对应的，小根堆可将数组降序排序)

关于堆的内容，参看数据结构部分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<iostream>
using namespace std;
const int N = 100010;
int q[N]; //待排序数组
int n;  //数组长度
int length;//堆当前长度
void down(int q[], int x)
{
    int maax = x;
    if(x*2 <= length&&q[x*2]>q[maax]) maax = x*2;
    if(x*2+1 <= length && q[x*2+1]>q[maax]) maax = x*2+1;
    if(x!=maax)
    {
        swap(q[x],q[maax]);
        down(q, maax);
    }
}

void create(int q[]) //将数组转化为大顶堆
{
    for(int i = length/2;i>0;i--) down(q, i);
}

void pop(int q[]) //弹出堆顶元素
{
    swap(q[1], q[length]);
    length--;
    down(q, 1);
}

void HeapSort(int q[])
{
    create(q); 
    while(length) pop(q);
}

int main()
{
    scanf("%d",&n);
    length = n;
    for(int i = 1;i<=n;i++) scanf("%d", &q[i]);
   HeapSort(q);
    for(int i = 1;i<=n;i++) printf("%d ", q[i]);
    return 0;
}

分析
时间复杂度：平均$nlogn$，最好$nlogn$，最坏$nlogn$
空间复杂度：$O(1)$，所有操作均在给定数组上完成
稳定性：不稳定

4. 归并排序

  1. 确定分界点mid=（l-r）/2，把数组分为左右两部分
  2. 对左右两部分分别递归
  3. 归并（递归触底开始释放时，原数组的每一个元素都被拆分为一个个只有一个元素的数组，因此它们都是有序的，而归并操作又是一个排序的过程，所以每一次进行归并操作的两个数组都是有序的）

关键在于第三步归并，假定待排序数组为arr[ ]。
创建一个数组temp[ ]用来放每次递归排好序的数组，左数组和右数组归并比较，把结果存入temp[ ]。最后把temp[ ]的内容放回到arr[ ]中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;
    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);
    int k = 0, i = l, j = mid + 1;   //k为临时数组的指针
    while (i <= mid && j <= r)       //归并排序
    {
        if (q[i] < q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];
    }
    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];
    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j]; //内容放回原数组
}

分析
时间复杂度：最好最坏平均都是$O(nlogn)$
空间复杂度：$O(n)$
稳定性：稳定

4.1 求逆序对的数量（归并排序应用）

逆序对：数组下标i<j，但value[i]>value[j]，则(value[i], value[j])就被称为该数组的一个逆序对。
我们知道归并操作开始时，两个被mid分割的数组分别有序。我们使用指针i和j分别操作这”两个”数组（i从l到mid，j从mid+1到r）。在它们合并为一个新数组的一次操作中，如果a[j]比a[i]小，则它比a[i]到a[mid]所有的元素都小，且比a[l]到a[i-1]的所有元素都大，据此我们可以得到a[j]相对于左边数组的逆序对数量：mid-i+1（即i到mid的长度）。另外归并操作是从两个1-1数组开始的，所以从一开始我们就可以假定函数可以返回对应区间所有元素的逆序对数量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<iostream>
using namespace std;
const int N = 100050;
typedef long long ll;
int q[N];
int temp[N];
int n;

/*因为逆序对的数量可能很多，最好用long long*/
ll merge_find(int l, int r, int q[])
{
    if(l>=r) return 0; 
    int mid = l+r>>1;
    ll res = merge_find(l, mid, q) + merge_find(mid+1, r, q);
    
    /*归并*/
    int k = 0;
    int i = l, j = mid+1;
    while(i<=mid&&j<=r)
    {
        if(q[i]<=q[j]) temp[k++] = q[i++];
        else 
        {
            temp[k++] = q[j++];
            /*当q[j]比q[i]小时，它比q[i]到q[mid]的所有
            元素都小，q[j]关于左侧数组的逆序对数量就是
            这段区间的长度*/
            res += mid-i+1; 
        }
    }
    while(i<=mid) temp[k++] = q[i++];
    while(j<=r) temp[k++] = q[j++];
    for(int i = l, j = 0; i<=r; i++, j++) q[i] = temp[j];
    return res;
}

int main()
{
    scanf("%d",&n);
    for(int i = 0;i<n;i++) scanf("%d", &q[i]);
    ll re = merge_find(0, n-1, q);
    printf("%lld\n",re);
    return 0;
}

5. 基数排序

总的来看，原理是（只讨论排正整数）将数组中的数从低位到高位分别排序。
具体地，创建10个桶（队列），分别代表0~9，将当前待排序位数上的值存入对应的桶，一趟排完后，从左到右，从小到大将队列中的值存放到原数组中，形成新的序列。不断重复以上过程，直到将最大位数排序完毕，即得到有序数列。
该算法速度很快，但限制较大（比如最大位数差不能过大）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//假定待排序数组内都是位数小于等于digit的正整数
void sort(int a[], int length, int digit)
{
   queue<int> q[10]; //10个桶，对应0~9
   for(int i = 1, count = 0;count<digit; i*=10,count++) //从低位到高位
   {
       for(int j = 0; j<length;j++) //遍历数组a，对每个数的位i上的值排序
       {
           int value = (a[j]/i)%10; //获取位i上的值
           q[value].push(a[j]); //将该元素放到对应的桶中
       }

       int location = 0;
       for(int k = 0;k<10;k++) //从左到右，从小到大将所有桶的元素覆盖到原数组中
       {
           while(!q[k].empty())
           {
               a[location++] = q[k].front();
               q[k].pop();
           }
       }
       /*
       打印过程
       for(int p = 0;p<length;p++) printf("(%d) ", a[p]);
       cout<<endl;
       */
   }
}

分析
时间复杂度：平均$O(n\times digit)$，最好$O(n\times digit)$，最坏$O(n\times digit)$。其实都是$O(n)$，只不过digit较大时对效率的影响也较大，故写出。
空间复杂度：$O(digit)$
稳定性：稳定

总结

n较小，数据较乱，使用选择排序；若数据基本有序，使用直接插入或者冒泡。
n较大，若不要求稳定，优先快排；若要求稳定，使用归并；
n较大，若数组元素都为正整数且位数差较小，使用基数排序很快。