《字符串》专题

Posted on Edited on In , Views:

0. KMP

高效的字符串匹配算法（在母串s中匹配模式串p）。
对于字符串匹配问题，如果采用暴力算法，也就是p逐位的与s比较，一旦中途某字符不匹配，p就前进1格，重新与s逐位比较，它的时间复杂度为O(n^n），n为字符串长度。
而事实上我们可以利用已知信息让p跳跃式的前进，降低时间复杂度，这就是KMP算法的目的。
注：自己对着代码手动模拟一遍能够降低理解难度

0.1 模拟样例

假如模式串p为[a, b, d, a, b, b]，母串为[b, a, b, d, a, b, c]

当匹配进行到这一步时，暴力做法是模式串右移一位，重新从头逐位与母串匹配

但我们发现在模式串中，与母串不匹配位置（上图圆圈处）左侧的子串中，存在最大公共前后缀（下图连线标出）

前缀: 从字符串首字符开始不包含最后一个字符的所有可能的连续子串
后缀: 字符串中不包含首字符的且以最后一个字符结尾的所有可能子串

找出模式串中的最大公共前后缀有啥意义呢？它可以帮我们实现模式串p的跳跃前进（发生某字符不匹配情况时，p可直接跳到它的最大公共后缀处开始新的匹配），且中间不会漏解（注意一定是最大的公共前后缀才能确保不会漏解），效果如下

以上就是kmp算法的原理了，道理很简单，既然模式串中某部分与母串匹配了，且这部分存在最大公共前后缀，那么在这对前后缀之间就不可能存在匹配的情况了（否则后缀就应该位于这个匹配的情况所在位置），因此可以直接把模式串移到后缀位置。
概括来看：

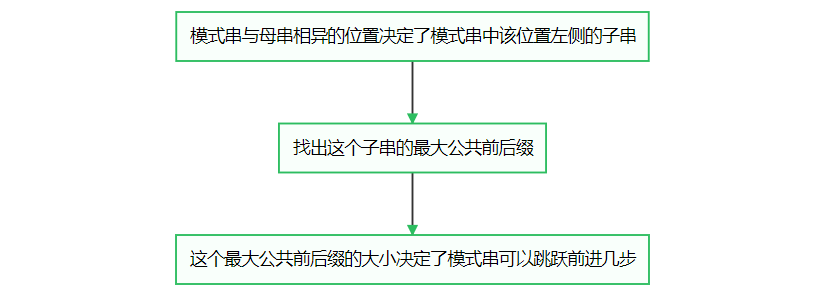
这样看来，我们可以在进行字符串匹配之前，预处理出模式串的信息：对模式串中每一个位置，先假定它与母串不匹配，得到这个位置左侧子串的最大公共前后缀，并由此拿到模式串在该位置如果与母串不匹配的话，可以跳跃前进几步的信息。
如果预先得到这样一个关于模式串某位置与母串不匹配时可以跳跃前进几步的数组（一般称为next数组），再进行字符串匹配，就能在匹配的过程中利用next数组提供的信息使得模式串能够跳跃式前进。

0.2 模板

0.2.1 创建next数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/*构造next数组*/
void getNext() 
{ //从可能的最长的公共前后缀开始找，j指向当前公共前缀的末尾，i指向当前公共后缀的末尾 
    ne[0] = -1;
    for(int i = 1, j = -1; i<pLength; i++) //为什么i从1开始j从-1开始？想想可能的最长公共前后缀是什么样子
    { 
        /*如果当前【公共前缀末尾的下一个位置元素】与【后缀指针当前位置】元素不匹配，
        则j退回到当前公共前缀数组的前缀的后一位（因为前缀数组本身也有公共前后缀）。
        其实这一步是做了优化，其本质就是令j不断回退，一直退回到p[i]=p[j+1]的位置就停止。*/
        while(j>=0&&p[i]!=p[j+1]) j = ne[j]; 
        //只有当公共【前缀末尾的下一个位置元素】与【后缀指针当前位置】元素匹配时，j所代表的前缀数组才会向右扩大 
        if(p[i]==p[j+1]) j++; 
        //j当前所在位置，就是与以i结尾的后缀数组相匹配的前缀数组末尾
        //ne[i]=j 表示当模式串与母串在i处不匹配时，模式串可以向右一次跳跃j个下标
        ne[i] = j; 
    }
}

栗子

当前匹配进程如下

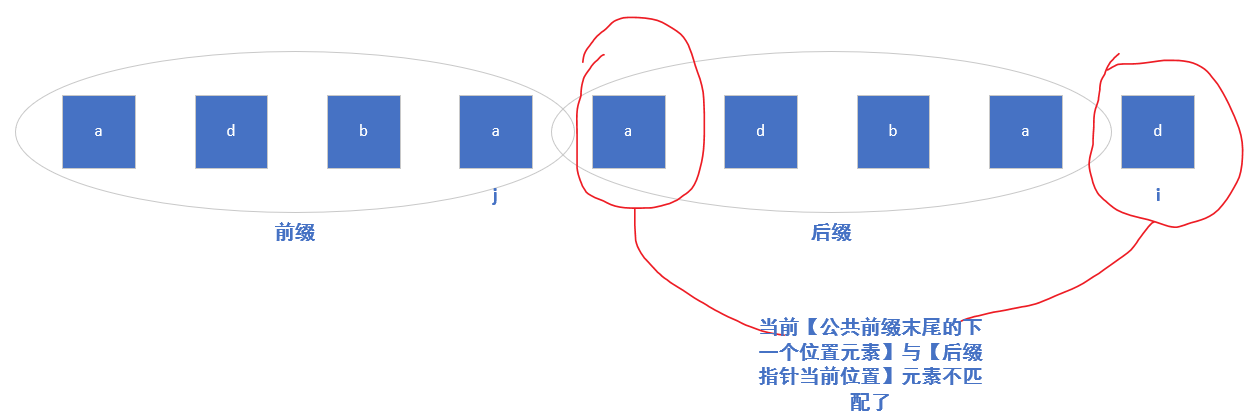
前后缀数组的下一个元素不匹配了，现在我们要做的是对前缀从右往左收缩，对后缀从左往右收缩，直到它们再次相等，才能开始下一次比对。

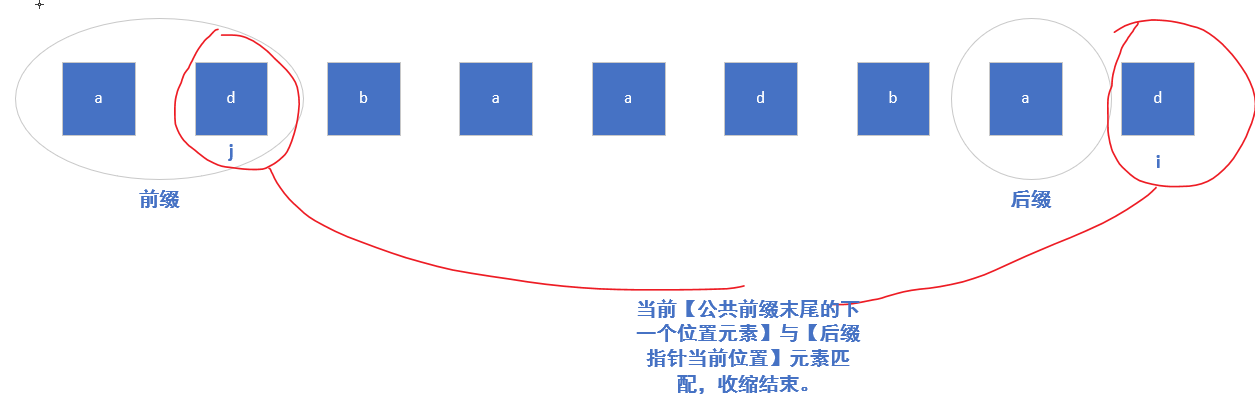
因为收缩开始前的前后缀数组是相同的，所以它们各自的最大公共前后缀也是相同的，因此回退可以是跳跃式的：j退回到前缀数组中最大前缀的末尾位置，即j = ne[j]。

然后继续匹配：

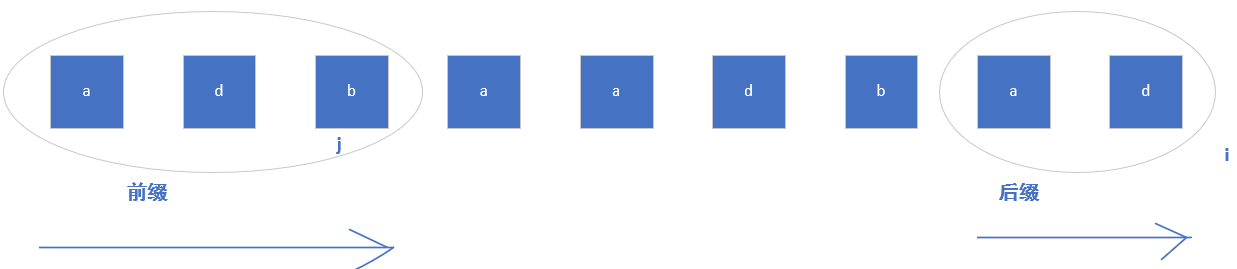
上图是回退一次就相同的情况，如果回退一次j的下一个位置元素还是与i位置元素不同，则需要再令j=ne[j]回退，直到相同或者j<0时结束，此时j所在位置就是当字符串与模式串第i个字符不匹配时，模式串可以向右跳跃的步数。

0.2.2 使用next数组完成字符串匹配

s为母串，p为模式串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//i为母串指针，j为模式串指针
for(int i = 0,j=-1;i<sLength;i++) 
    { 
        //如果当前【模式串的下一个位置元素】与【母串当前位置元素】不匹配
        //j退回到以它结尾的前缀的最大公共前缀末尾，但因为i不变，所以这句话其实相当于把模式串和母串当前已完成
        //匹配部分的子串的公共后缀找出来，然后直接把模式串前缀移动到这个公共后缀处，完成跳跃前进
        while(j>=0&&s[i]!=p[j+1]) j = ne[j]; 
        
        if(s[i]==p[j+1]) j++; //模式串当前匹配了多少位母串
        
        if(j==pLength-1) //如果整个模式串匹配完毕 
        { //本次在母串中成功匹配的模式串起始下标为i-j 
            printf("%d ", i-j);
            j = ne[j]; //不写这句也能AC，不过因为这条指令之后就是【while(j&&s[i]!=p[j+1]) j = ne[j];】有j+1，为了避免边界问题还是加上
        }
    }

把字符串移动到它最大公共后缀开始的位置，反映到代码上就是把指向字符串的指针移动到它最大公共前缀的末尾

0.3 例题

给定一个母串S，以及一个模式串P，所有字符串中只包含大小写英文字母以及阿拉伯数字。模式串P在母串S中多次作为子串出现。求出模式串P在母串S中所有出现的位置的起始下标。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include<iostream>
using namespace std;
const int N = 1000010;
char s[N];  //母串
char p[N];  //模式串
int ne[N];  //next数组，初始为全0
int pLength, sLength; //模式串长度，母串长度

/*该算法默认所有数组下标从1开始，这样格式能够统一*/

/*获取next数组*/
void getNext() 
{ //从可能的最长的公共前后缀开始找，j指向当前公共前缀的末尾，i指向当前公共后缀的末尾 
    ne[0] = -1;
    for(int i = 1, j = -1; i<pLength; i++) 
    { 
        //如果当前公共【前缀末尾的下一个位置元素】与【后缀当前位置】元素不匹配
        //则j退回到当前公共前缀数组的前缀的后一位（因为前缀数组本身也有公共前后缀）
        while(j>=0&&p[i]!=p[j+1]) j = ne[j]; 
        //只有当公共【前缀末尾的下一个位置元素】与【后缀当前位置】元素匹配时，j所代表的前缀数组才会向右扩大 
        if(p[i]==p[j+1]) j++; 
        //j当前所在位置，就是与以i结尾的后缀数组相匹配的前缀数组末尾
        //ne[i]=j 表示当模式串与母串在i处不匹配时，模式串可以向右一次跳跃j个下标
        ne[i] = j; 
    }
}

int main()
{
    cin>>pLength>>p>>sLength>>s; //用于记录母串和模式串的数组下标均从1开始
    
    getNext(); //构造出模式串的next数组
    
    //i为母串指针，j为模式串指针
    for(int i = 0,j=-1;i<sLength;i++) 
    { 
        //如果当前【模式串的下一个位置元素】与【母串当前位置元素】不匹配
        //j退回到以它结尾的前缀的最大公共前缀末尾，但因为i不变，所以这句话其实相当于把模式串和母串当前已完成
        //匹配部分的子串的公共后缀找出来，然后直接把模式串前缀移动到这个公共后缀处，完成跳跃前进
        while(j>=0&&s[i]!=p[j+1]) j = ne[j]; 
        
        if(s[i]==p[j+1]) j++; //模式串当前匹配了多少位母串
        
        if(j==pLength-1) //如果整个模式串匹配完毕 
        { //本次在母串中成功匹配的模式串起始下标为i-j 
            printf("%d ", i-j);
            j = ne[j]; //不写这句也能AC，不过因为这条指令之后就是【while(j&&s[i]!=p[j+1]) j = ne[j];】有j+1，为了避免边界问题还是加上
        }
    }
    
    return 0;
}

1. 寻找公共字符

【题目】

Given an array A of strings made only from lowercase letters, return a list of all characters that show up in all strings within the list (including duplicates). For example, if a character occurs 3 times in all strings but not 4 times, you need to include that character three times in the final answer.

You may return the answer in any order.

Example 1:

Input: [“bella”,”label”,”roller”]
Output: [“e”,”l”,”l”]

Example 2:

Input: [“cool”,”lock”,”cook”]
Output: [“c”,”o”]

【解析】

因为题目说明了所有字符串都是由小写字母组成的，因此可以用长度为26的数组（桶）来标识字符串中每一个字母出现的频率。

先用桶A记录第一个字符串中所有字母出现的频率。然后遍历所有其他字符串，对每一个字符串用一个桶B记录其字母频率，每次记录完一个字符串的字母频率，就对比A和B中的每条记录，把 较小的记录更新到桶A中，继续迭代，直到所有字符串都被比较完毕后，桶A中存储的数据就是答案（桶A的下标i+’a’对应小写字母，下标处的值对应该小写字母在所有字符串中是否都出现过，出现了几次）

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
private:
    vector<string> re; //存储答案
public:
    vector<string> commonChars(vector<string>& A) {
        
        int mark[26] = {0}; //第一个桶
      	//记录第一个字符串的字母出现频率
        for(int i = 0;i<A[0].size();i++) mark[A[0][i]-'a']++;
       

        int otherMark[26] = {0}; //第二个桶
        for(int i = 1; i<A.size(); i++)
        {
            memset(otherMark, 0 ,sizeof(otherMark)); //旧桶翻新
            //记录其他字符串的字母出现频率
            for(int j = 0; j<A[i].size(); j++) otherMark[A[i][j]-'a']++;
          	//比较第一个桶和第二个桶中的数据，取它们字母出现频率的较小值，更新到第一个桶中
            for(int k = 0;k<26;k++) mark[k] = min(mark[k], otherMark[k]);
        }
        
        /*此时mark中存储的就是每一个小写字母在所有字符串中出现的频率，将其转化为题目要求的格式放入答案数组*/
        for(int i = 0;i<26;i++) //遍历所有小写字母i+'a'
        {
            for(int j = 0; j<mark[i]; j++) //如第该字母在所字符串中出现了mark[i]次，将其放入答案数组中
            {
                string s = string(1, i+'a'); 
                re.push_back(s);
            }
        }
        return re;
    }
};

2. 比较带退格符的两字符串

【题目】

Given two strings S and T, return if they are equal when both are typed into empty text editors. # means a backspace character.

Note that after backspacing an empty text, the text will continue empty.

Example 1:

Input: S = “ab#c”, T = “ad#c”
Output: true
Explanation: Both S and T become “ac”.

Example 2:

Input: S = “ab##”, T = “c#d#”
Output: true
Explanation: Both S and T become “”.

Example 3:

Input: S = “a##c”, T = “#a#c”
Output: true
Explanation: Both S and T become “c”.

Example 4:

Input: S = “a#c”, T = “b”
Output: false
Explanation: S becomes “c” while T becomes “b”.

Note:

1 <= S.length <= 200
1 <= T.length <= 200
S and T only contain lowercase letters and '#' characters.

【解析】

将字符串的字符逐个入栈，只要碰到”#“就弹栈，最后比较两个字符串的栈，如果相同就返回true，不同就返回false

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    bool backspaceCompare(string S, string T) {
        int sLength = S.size();
        int tLength = T.size();
        stack<char> ss, tt;
        
        /*利用栈将两个字符串的退格符处理掉*/
        for(int i = 0;i<sLength;i++) 
        {
            if(S[i]!='#') ss.push(S[i]);
            else if(!ss.empty()) ss.pop();
        }
        for(int i = 0;i<tLength;i++)
        {
            if(T[i]!='#') tt.push(T[i]);
            else if(!tt.empty()) tt.pop();
        }
        
        if(tt.size()!=ss.size()) return false; //如果两个栈长度不等，直接返回false
        
        /*比较两个栈是否相同*/
        int ttLength = tt.size();
        for(int i = 0;i<ttLength;i++)
        {
            int value1 = tt.top(); tt.pop();
            int value2 = ss.top(); ss.pop();
            if(value1!=value2) return false;
        }
        return true;
    }
};

3. 划分字母区间

【题目】

简单的说，就是给定一个纯小写字母字符串，让我们划分出【最多】个区间，每个区间中的字母都仅在本区间中出现

【解析】

一开始先找到第一个字母（位置begin）在字符串中最后出现的位置end，则begin和end形成一个窗口，遍历这个窗口中的所有字母并逐个计算它们在整个字符串中最后出现的位置，如果过程中有字母的最后出现位置大于end，则将end更新。窗口遍历到end时，该窗口就是一个最小partition，其长度为end-begin+1。接着令begin=end+1，开始寻找下一个partition。

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
public:
    /*返回字母c在字符串S中最后一次出现的位置*/
    int LastPos(string S, char c)
    {
        int length = S.size();
        for(int i = length-1;i>=0;i--)
        {
            if(S[i] == c) return i;
        }
        return -1;
    }
    
    vector<int> partitionLabels(string S) {
        int length = S.size();
        vector<int> re;
        if(length==0) return re;
        if(length==1) 
        {
            re.push_back(1);
            return re;
        }
        
        
        int end=0;
        int update = 0;
        /*partition操作*/
        for(int begin = 0; begin<length;)
        {
            end = LastPos(S, S[begin]); //先寻找begin位置上的字母在字符串最后出现位置，形begin~end的窗口
            /*遍历当前窗口中的每一个字母*/
            for(int j = begin+1; j<end; j++)
            {
                update = LastPos(S, S[j]); //计算当前字母在字符串中最后出现位置
                if(update==-1) continue; //如果当前字母在字符串中唯一存在，则它必然不会导致end更新，跳过
                end = max(end, update);	//如果当前字母的最后出现位置大于end，则更新end
            }
            //当前窗口遍历完毕后，就得到了一个partition，end-begin+1就是该partition的长度
            re.push_back(end-begin+1); 
            
            begin = end+1;//开始寻找下一个partition
        }
        return re;
    }
};

4. 移掉k位数字

【题目】

给定一个以字符串表示的非负整数 num，移除这个数中的 k 位数字，使得剩下的数字最小。

注意:

num 的长度小于 10002 且 ≥ k。
num 不会包含任何前导零。

示例 1 :

输入: num = “1432219”, k = 3
输出: “1219”
解释: 移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219。

示例 2 :

输入: num = “10200”, k = 1
输出: “200”
解释: 移掉首位的 1 剩下的数字为 200. 注意输出不能有任何前导零。

示例 3 :

输入: num = “10”, k = 2
输出: “0”
解释: 从原数字移除所有的数字，剩余为空就是0。

【解析】

先将loc定为0，然后在[loc, k]之间选择一个最小的数作为答案的最高位，并把loc移动到这个最小的数所在位置。

在[loc+1, k+1]之间选择一个最小的数作为答案的次高位，并把loc移动到这个最小的数所在位置。

在[loc+1, k+1]之间选择一个最小的数作为答案的次次高位…..

直到k==length时，结束。

最后将前导零消除即可得到答案。

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    string removeKdigits(string num, int k) {
        string re;		   //答案
        vector<char> tmp;  //未消除前导零的答案
        int length = num.size();
        int loc = -1;
        while(k!=length) //当k==length时就得到答案了
        {
            int miin = 11; //将miin初始化为“无穷大”
            for(int i = loc+1;i<=k;i++) //在[loc+1, k]之间寻找最小值
            {
                if(miin>num[i]-'0')
                {
                    miin = num[i]-'0';
                    loc = i;
                }
            }
            tmp.push_back(miin+'0'); //将最小值存入tmp数组
            k++;
        }
        
        /*消除前导零*/
        int count0 = 0;
        int i = 0;
        for(int i = 0;i<tmp.size();i++)
        {
            if(tmp[i]!='0') break;
            else count0++;
        }
        if(count0==tmp.size()) return "0";
        re.assign(tmp.begin()+count0, tmp.end());
        
        
        return re;
    }
};

5. 上升下降字符串

【题目】

给你一个字符串 s ，请你根据下面的算法重新构造字符串：

从 s 中选出 最小 的字符，将它 接在 结果字符串的后面。
从 s 剩余字符中选出 最小 的字符，且该字符比上一个添加的字符大，将它 接在 结果字符串后面。
重复步骤 2 ，直到你没法从 s 中选择字符。
从 s 中选出 最大 的字符，将它 接在 结果字符串的后面。
从 s 剩余字符中选出 最大 的字符，且该字符比上一个添加的字符小，将它 接在 结果字符串后面。
重复步骤 5 ，直到你没法从 s 中选择字符。
重复步骤 1 到 6 ，直到 s 中所有字符都已经被选过。

在任何一步中，如果最小或者最大字符不止一个 ，你可以选择其中任意一个，并将其添加到结果字符串。

请你返回将 s 中字符重新排序后的 结果字符串 。

示例 1：

输入：s = “aaaabbbbcccc”
输出：”abccbaabccba”
解释：第一轮的步骤 1，2，3 后，结果字符串为 result = “abc”
第一轮的步骤 4，5，6 后，结果字符串为 result = “abccba”
第一轮结束，现在 s = “aabbcc” ，我们再次回到步骤 1
第二轮的步骤 1，2，3 后，结果字符串为 result = “abccbaabc”
第二轮的步骤 4，5，6 后，结果字符串为 result = “abccbaabccba”

示例 2：

输入：s = “rat”
输出：”art”
解释：单词 “rat” 在上述算法重排序以后变成 “art”

示例 3：

输入：s = “leetcode”
输出：”cdelotee”

示例 4：

输入：s = “ggggggg”
输出：”ggggggg”

示例 5：

输入：s = “spo”
输出：”ops”

提示：

1 <= s.length <= 500
s 只包含小写英文字母。

【解析】

题目要求我们来回地遍历字符串，每次遍历都要取出一些字符放到结果字符串，而且取出字符的过程还必须按照 字典序，最终还要判断原字符串是否被取完。如果完全按照题目要求做时间复杂度是非常高，且代码实现也是比较复杂的。

因为题目规定字符串中的字符都为小写字母，所以我们可以用桶的思想来做。

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    string sortString(string s) {
        string re;
        
        /*把字符串中所有字符放入桶中，这样就天然符合字典序了，而且将字符从原字符串中取出这个操作只需要对桶进行自减操作即可实现*/
        int bucket[27] = {0};
        for(int i = 0;i<s.size();i++) bucket[s[i]-'a']++;
        
        int length = s.size();
        while(length) //当原字符串中的字符串没有被取完时
        {
            for(int i = 0;i<27;i++) //按字典升序从原字符串中无重复地取出字符追加到结果字符串中
            {
                if(length && bucket[i]) //如果桶i的计数大于1，说明原字符串中还有i+'a'这个字符
                {
                    re.push_back(i+'a'); //将i+'a'追加到结果字符串中
                    bucket[i]--; 		//该操作相当于将字符i+'a'从原字符串中删除
                    length--;			//原字符串长度自减
                }
            }
            for(int i = 26;i>=0;i--)//按字典降序从原字符串中无重复地取出字符追加到结果字符串中
            {
                if(length && bucket[i])
                {
                    re.push_back(i+'a');
                    bucket[i]--;
                    length--;
                }
            }
        }

        return re;
    }
};

总结，以下情况要考虑使用桶：

  1. 按字典序或者数字大小的顺序从乱序的数组中多次取出元素
  2. 要多次从【删除操作复杂度高的数据结构中进行删除操作】
  3. 多次遍历一个【数据范围较小的类数组结构（如字符串），且其中可能存在较多的重复元素】

6. 无重复字符的最长字符串

【题目】

给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。

示例 2:

输入: s = “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”，所以其长度为 1。

示例 3:

输入: s = “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”，所以其长度为 3。
请注意，你的答案必须是 子串 的长度，”pwke” 是一个子序列，不是子串。

【解析】

在暴力做法的基础上可以进行一些优化。

设置一个窗口[left, right]，初始为[0, 0]。在right右移的过程中，不断的判断窗口内[left, right-1]中有没有元素与下标为right的元素相等（同时对不等的元素计数），如果有，把left拉到这个元素之后即可（即以后的判断都可以跳过这个重复的部分）。

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int length = s.size();
        if(length==0) return 0;
        
        int maax = 1;//只要不是空字符串，则无重复字符的最长子字符串至少长为1


        int left = 0;//窗口左端点
        for(int right = 1;right<length;right++)//窗口右端点不断右移
        {
            int count = 1; //计算当前最长无重复字符的字符串长度
            for(int j = right-1;j>=left;j--) //在[left, right-1]中寻找有没有与下标为right元素相同的元素
            {
                if(s[j]==s[right]) //如果有
                {
                    left = j+1; //把窗口左端点直接移到重复元素之后
                    break;      //直接开始下次迭代
                }
                count++; //对不相等的元素计数
            }
            maax = max(maax, count); //要求取最长字符串
        }
        return maax;
    }
};

7. 同构字符串

【题目】

给定两个长度相同的字符串 s 和 t，判断它们是否是同构的。

如果 s 中的字符可以被替换得到 t ，那么这两个字符串是同构的。

所有出现的字符都必须用另一个字符替换，同时保留字符的顺序。两个字符不能映射到同一个字符上，但字符可以映射自己本身。

示例 1:

输入: s = “egg”, t = “add”
输出: true

示例 2:

输入: s = “foo”, t = “bar”
输出: false

示例 3:

输入: s = “paper”, t = “title”
输出: true

【解析】

本题关键在于如何统一的标识两个字符串的结构。我们可以同时遍历两个字符串，在遍历的过程中，将当前指针所在下标作为两个字符串中该下标处元素的标识（即用两个哈希表分别存储两个字符串的结构信息：当前位置元素为key，当前位置下标为value），每走到一个新的位置i，就判断两字符串中该位置的元素的上一次出现位置是否相同，如果不相同说明不同构，如果相同就将它们的上一次出现位置更新为i。

【ac代码】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    bool isIsomorphic(string s, string t) {
        char s_hash[256] = {0}, t_hash[256] = {0}; //两个哈希表分别记录两个字符串的结构
        int length = s.size();
        for(int i = 0;i<length;i++){
            if(s_hash[s[i]]!=t_hash[t[i]]) return false; //这一次s[i]和t[i]出现在两个字符串中的对应位置，那么s[i]和t[i]上一次在各自字符串中出现的位置也必然对应，否则字符串s和t一定不同构
            //用当前遍历到的位置i来记录s[i]和t[i]这两个元素的出现位置
            s_hash[s[i]] = i+1; 
            t_hash[t[i]] = i+1;
        }
        return true;
    }
};